9 - grafi pesati, algoritmo di Dijkstra

grafo pesato

Un grafo $G$ è detto pesato se ad ogni arco $e\in E$ è associato un valore numerico (detto peso) (funzione $w:E\to R$ associa ad ogni arco un peso).

• il peso di un cammino $P$ è dato dalla somma dei pesi degli archi che lo costituiscono

Per rappresentare un grafo pesato tramite lista di adiacenza, per l’arco $(x,y)$ di peso $c$ nella lista di adiacenza di $x$, invece che il solo nodo di destinazione $y$, ci sarà la coppia $(y,c)$.

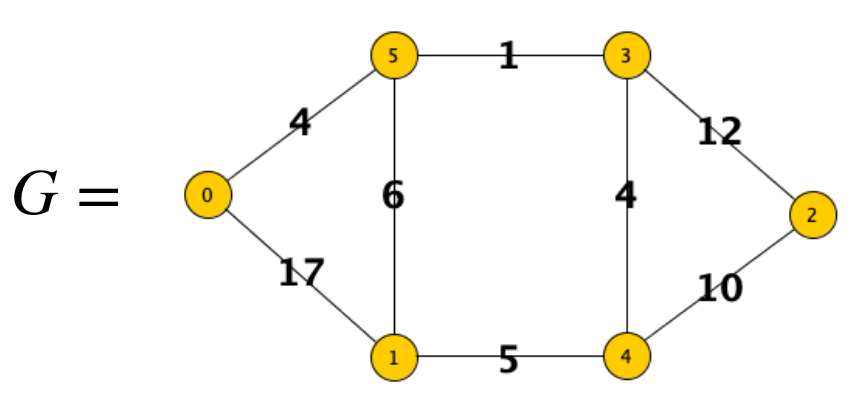
il grafo sopra avrà lista di adiacenza:

G = [
	[(1, 17), (5, 4)],
	[(0, 17), (4, 5), (5, 6)],
	[(3, 12), (4, 10)],
	[(2, 12), (4, 4), (5, 1)],
	[(1, 5), (2, 10), (3, 4)],
	[(0, 4), (1, 6), (3, 1)]
]

analogia dei contenitori d'acqua

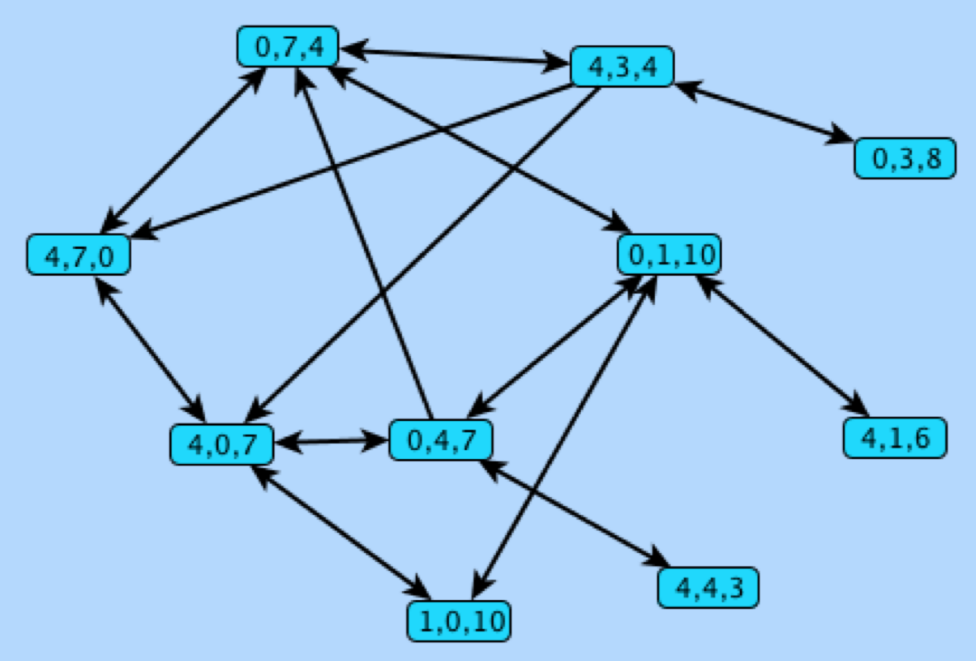
Abbiamo tre contenitori d’acqua con capienza 4, 7 e 10 litri. Inizialmente, i contenitori da 4 e 7 litri sono pieni, mentre quello da 10 è vuoto. Possiamo fare un solo tipo di operazione: versare acqua da un contenitore ad un altro, fermandoci quando il contenitore sorgente è vuoto o quello destinazione pieno.

Vogliamo sapere se esiste una sequenza di operazioni di versamento che termina lasciando esattamente 2L di acqua nel contenitore da 4 o nel contenitore da 7.

Il problema si può modellare con un grafo $G$:

• i nodi di $G$ rappresentano i possibili stati di riempimento dei contenitori (tramite una configurazione $(a,b,c)$ dove le tre lettere rappresentano il numero di litri nei tre contenitori)
• c’è un arco tra un nodo $(a,b,c)$ a un nodo $(a^{\prime },b^{\prime },c^{\prime })$ se dallo stato $(a,b,c)$ è possibile passare allo stato $(a^{\prime },b^{\prime },c^{\prime })$ con un versamento lecito

Per risolvere il problema, basta chiedersi se nel grafo diretto $G$ almeno uno dei nodi $(2,\ast ,\ast )$ o $(\ast ,2,\ast )$ è raggiungibile a partire dal nodo $(4,7,0)$.

• per facilitare la ricerca, possiamo aggiungere un nodo pozzo $(-1,-1,-1)$ con archi entranti solo dai nodi $(2,\ast ,\ast )$ e $(\ast ,2,\ast )$, e chiederci se questo sia raggiungibile da $(4,7,0)$
• per raggiungere uno dei due target con il minimo numero di travasi ci basta effettuare una visita BFS per la ricerca dei cammini minimi, calcolando le distanze minime a partire da $(4,7,0)$ ($O(n+m)$)

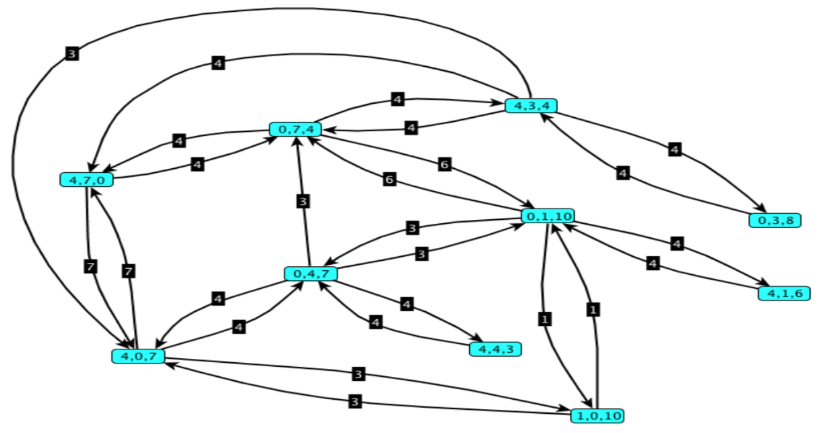
Consideriamo però questa variante del problema: consideriamo una sequenza di operazioni di versamento come buona se termina lasciando esattamente 2 litri in uno dei due contenitori. Inoltre, una sequenza buona è parsimoniosa se il totale dei litri versati in tutti i versamenti della sequenza è minimo rispetto a tutte le sequenze buone. Cerchiamo una sequenza buona e parsimoniosa.

Ci conviene aggiungere un costo ad ogni arco per rappresentare il numero di litri che vengono versati nella mossa corrispondente.

Trovare un cammino dal nodo $(4.7,0)$ al pozzo $(-1,-1,-1)$ che minimizzi la somma dei costi degli archi attraversati diventa una generalizzazione del problema dei cammini di lunghezza minima.

Possiamo infatti sostituire un arco da $x$ a $y$ di costo $C$ con un cammino con $C-1$ nuovi nodi - in questo modo, ogni arco corrisponde al versamento di 1L d’acqua, e contando gli archi di un cammino tra due nodi contiamo esattamente il numero di litri versati. Basta quindi eseguire una BFS nel nuovo grafo. Essa avrà complessità $O(n^{\prime }+m^{\prime })$ con $n^{\prime }$ e $m^{\prime }$ nodi e archi del nuovo grafo.

Abbiamo ricondotto un problema di cammini minimi su grafi pesati ad uno di cammini minimi in un grafo non pesato. Ma questo approccio è possibile solo quando gli archi hanno pesi interi e relativamente piccoli.

Esiste quindi un algoritmo che ci permette di risolvere il problema dei cammini minimi lavorando direttamente su grafi pesati.

algoritmo di Dijkstra

problema:

Dato un grafo pesato, vogliamo trovare i cammini minimi, e quindi anche le distanze da un nodo $s$ (sorgente) a tutti gli altri nodi del grafo.

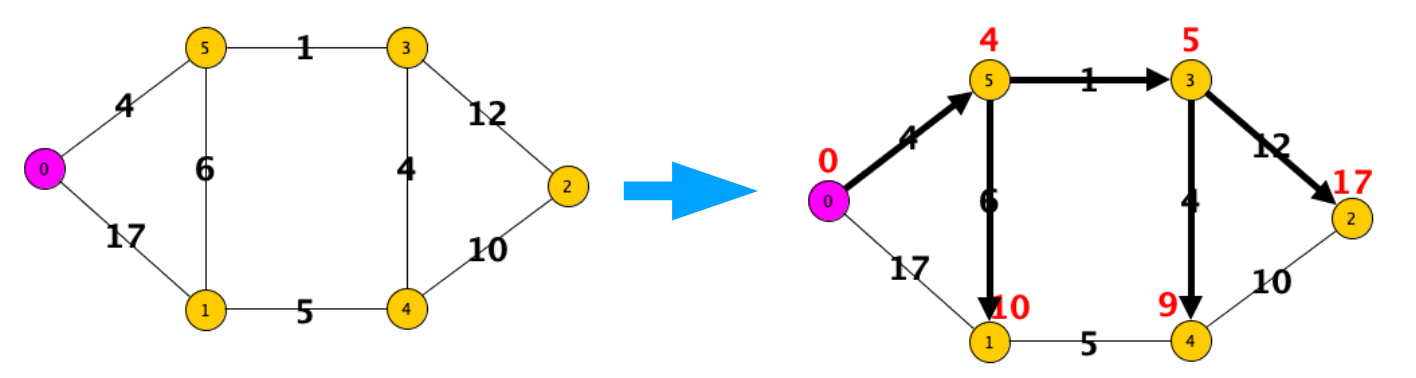
(^ cammini minimi dalla sorgente $0$ a tutti gli altri nodi)

L’algoritmo di Dijkstra costruisce l’albero dei cammini minimi un arco per volta partendo dal nodo sorgente, e segue questa logica:

• ad ogni passo, aggiunge all’albero l’arco che produce il nuovo cammino più economico
• assegna ad ogni nodo come distanza il costo del cammino (che dalla radice porta ad esso)

L’algoritmo rientra nel paradigma della tecnica greedy. Opera infatti secondo una sequenza di decisioni irrevocabili:

• il cammino dal nodo sorgente ad un nuovo nodo viene deicso ad ogni passo, senza più tornare sulla decisione
• le decisioni vengono prese in base ad un criterio locale: tra tutti i cammini percorribili, si sceglie quello che costa meno

implementazioni

È impossibile risolvere il problema in meno di $\Omega (n+m)$. Esistono tre implementazioni principali:

• una senza strutture dati, in $\Theta (n^2)$: è ottima nel caso dei grafi densi (in cui $m\in O(n^2)$), ma non nel caso di grafi sparsi ($m\in O(n)$)
• una che utilizza la Heap, in $O((n+m)\log n)$: funziona meglio nel caso di grafi sparsi, ma nel caso di un grafo denso è preferibile la prima
• una terza, che utilizza la Heap di Fibonacci, in $O(n\log n+m)$: la migliore in entrambi i casi (ma non trattata)

pseudocodice:

• P[0...n-1] vettore dei padri inizializzato a -1
• D[0...n-1] vettore delle distanze inizializzato a +inf (perché si utilizzerà la funzione min())
• D[s], P[s] = 0, s (la sorgente ha distanza zero da se stessa ed è padre di se stessa)
• while esistono archi (x,y) con P[x]!=-1 e P[y]==-1:
  • sia (x,y) quello per cui è minimo D[x] + peso(x,y)
  • D[y], P[y] = D[x] + peso(x,y), x (si sceglie il cammino, quindi la distanza del nuovo nodo sarà data dalla distanza del padre + il peso dell’arco, e il padre del nuovo nodo sarà il nodo corrente)

attenzione: l'algoritmo non è corretto nel caso di grafi con pesi anche negativi

Infatti, poiché sceglie il cammino meno costoso ad ogni passo, non considera il caso in cui si percorrerà prima un arco con peso maggiore per poi incontrare archi con pesi negativi (che abbasseranno quindi il costo totale).

prova di correttezza

dimostrazione

Si dimostra per induzione sul numero di iterazioni del while (che assegna una nuova distanza ad un nodo).

Dobbiamo dimostrare che la distanza assegnata è quella minima.

• caso base: al passo zero viene assegnata distanza zero alla sorgente (e, poiché non consideriamo il caso di pesi negativi, non c’è una distanza minore)
• ipotesi induttiva: assumiamo che i cammini costruiti fino al passo $i>0$ siano minimi

Sia $T_i$ l’albero dei cammini minimi costruito fino al passo $i>0$ e $(u,v)$ l’arco aggiunto al passo $i+1$. Per dimostrare che $D[v]$ è la distanza minima, basta mostrare che il costo di un eventuale cammino alternativo è sempre superiore o uguale a $D[v]$.

Sia $C$ un qualsiasi cammino $s\to v$ alternativo a quello presente nell’albero e $(x,y)$ il primo arco che incontriamo percorrendo $C$ all’indietro tale che $x$ è nell’albero $T_i$ e $y$ no (ovvero l’ultimo arco percorso dal cammino).

• per ipotesi induttiva (e poiché non consideriamo archi con pesi negativi) $costo(C)\ge Dist(x)+peso(x,y)$

Ma l’algoritmo ha scelto $(u,v)$ invece che $(x,y)$, quindi, in base alla regola con cui esso sceglie l’arco con cui estendere l’albero, si ha necessariamente $D[x]+p(x,y)\ge D[u]+p(u,v)$.

• da qui segue $costo(C)\ge D[x]+peso(x,y)\ge D[u]+p(u,v)=D[v]$

Il cammino alternativo ha quindi un costo superiore a $D[v]$.

implementazione tramite lista

Si può mantenere una lista in cui, per ogni nodo $x$ viene memorizzata una tripla $(\text{definitivo, costo, origine})$, in cui:

• definitivo ⇒ flag che assume valore $1$ se il costo per raggiungere $x$ è stato definitivamente stabilito (ovvero se l’algoritmo ha stabilito che non esiste un percorso migliore per arrivare al nodo $x$)
• costo ⇒ costo corrente minimo noto per raggiungere $x$ dalla sorgente $s$
  • all’inizio, viene inizializzato a $0$ per $s$ e a $\infty$ per tutti gli altri nodi
• origine ⇒ nodo “padre” lungo il cammino minimo dalla sorgente a $x$
  • inizializzato a $-1$

All’inizio, l’unico nodo dell’albero è la sorgente, quindi la lista è inizializzata così:

$$lista[x]=\{\begin{array}{ll}(1,0,s)& x=s\\ (0,costo,s)& (costo,x)\in G[s]\\ (0,+\infty ,-1)& \text{altrimenti}\end{array}$$

Seguono una serie di iterazioni dove vengono eseguiti questi passaggi:

1. selezione del nodo con costo minimo non definitivo: si scorre $Lista$ per individuare il nodo $x$ che non è ancora definitivo e che ha il costo corrente minimo ⇒ è il candidato per il quale il cammino minimo dalla sorgente è attualmente noto
2. verifica di terminazione: se il costo minimo trovato è $\infty$, significa che non esistono altri nodi raggiungibili non definitivi. Il ciclo si interrompe.
3. marcare $x$ come definitivo: la flag del nodo selezionato viene aggiornata a $1$ (il suo costo definitivo è stato fissato e non sarà più modificato)
4. aggiornamento dei vicini di $x$ : per ogni nodo $y$ adiacente a $x$, se $y$ non è ancora definitivo e il nuovo costo ottenuto passando per esso (ovvero $cost{o}_x+cost{o}_{(x,y)}$) è inferiore o uguale al costo attuale memorizzato per $y$, si aggiorna la terna di $y$

def dijkstra(s, G):
	n = len(G)
	Lista = [(0, float('inf'), -1)]*n
	Lista[s] = (1, 0, s) 
	
	for y, costo in G[s]:
		# aggiorno vicini di s
		Lista[y] = (0, costo, s)
	
	while True:
		minimo, x = float('inf'), -1
		# cerco il nodo non definitivo con costo minimo
		# considerati solo i vicini, gli altri avranno inf
		for i in range(n):
			if Lista[i][0] == 0 and Lista[i][1] < minimo:
				minimo, x = Lista[i][1], i
		
		if minimo == float('inf'):
			# non ci sono più nodi raggiunbili non definitivi
			break
		
		# rendo definitivo il nodo x
		definitivo, costo_x, origine = Lista[x]
		Lista[x] = (1, costo_x, origine)
		
		# aggiornamento vicini
		for y, costo_arco in G[x]:
			# se y non è definitivo e  c'è un cammino migliore passando per x
			if Lista[y][0] == 0 and minimo + costo_arco < Lista[y][1]:
				Lista[y] = (0, minimo + costo_arco, x)
	
	# estrae vettori delle distanze e dei padri
	D,P = [costo for _,costo,_ in Lista], [origine for _,_,origine in Lista]
	return D, P

• il costo delle istruzioni al di fuori del while è $\Theta (n)$.
• il while viene eseguito al più $n-1$ volte (ad ogni iterazione un nuovo nodo viene selezionato e reso definitivo). Al suo interno:
  • il primo for viene eseguito esattamente $n$ volte
  • il secondo for viene eseguito al più $n$ volte (tante quanti sono gli adiacenti)

Il costo del while è quindi $\Theta (n^2)$, che è anche la complessità dell’implementazione.

[ TODO: inserire passaggi esempio ]

implementazione con Heap

Questa implementazione si basa sull’intuizione per cui, se si evitasse di scorrere ogni volta il vettore $lista$ per trovare il minimo, si eviterebbe di pagare $\Theta (n)$ ad ogni iterazione del while.

• si può quindi sostituire $lista$ con una Heap, che ha complessità $\log n$ per l’estrazione del minimo e per l’inserimento

Manteniamo un heap minimo contenente triple $(costo,u,v)$, dove $u$ è un nodo già inserito nell’albero dei cammini minimi e $costo$ rappresenta la distanza che si avrebbe qualora il nodo $y$ venisse inserito nell’albero dei cammini minimi attraverso $x$.

• ogni volta che aggiungiamo un nodo $x$ all’albero, aggiorniamo anche l’heap inserendo, per ogni vicino $y$ di $x$, una nuova tripla $(distanzaaggiornata,x,y)$
• dato che non rimuoviamo elementi già presenti nell’heap, possono esistere più entry dello stesso nodo con distanze differenti. Tuttavia, sappiamo che la prima volta che un nodo viene estratto, questa corrisponde alla distanza minnima calcolata fino a quel punto (quindi le successive estrazioni possono essere trascurate).
  • quindi, ad ogni estrazione di un nodo controlliamo prima se esso è già stato aggiunto all’albero (e, in tal caso, ignoriamo l’estrazione)

from heapq import heappush, heappop
 
def dijkstra1(s, G):
	n = len(G)
	D = [float('inf')]*n
	P = [-1]*n
	D[s] = 0
	P[s] = s
	H = [] # min-heap
	
	# inizializzazione heap (con vicini di s)
	for y, costo in G[s]:
		heappush(H, (costo, s, y))
	
	while H:
		# estraggo il nodo con distanza minore
		costo, x, y = heappop(H)
		if P[y] == -1:
			P[y] = x
			D[y] = costo
			
			for v, peso in G[y]:
				if P[v] == -1:
					heappush(H, (D[y]+peso, y, v))
	
	return D, P

Nella heap ci possono essere anche $O(m)$ elementi, quindi i costi di inserimento ed estrazione saranno $O(\log m)=O(\log n^2)=O(2\log n)=O(\log n)$.

• l’inizializzazione di $D$ e $P$ costa $\Theta (n)$, e l’inserimento dei vicini di $s$ costa $O(n\log n)$.

il costo del while con al suo interno un for è dato invece da:

• ad ogni iterazione del while si elimina un elemento da $H$ e, eventualmente, tramite il for annidato si scorre la lista di adiacenza di un nodo e si aggiungono elementi ad $H$. Ogni lista di adiacenza può essere scorsa al più una volta, quindi ad $H$ possono essere aggiunti al massimo $O(m)$ elementi. Il numero di iterazioni del while è quindi $O(m)$.
• escludendo il for annidato, il costo di ciascuna iterazione del while è $O(\log n)$ a causa dell’estrazione da $H$ - quindi, senza il for, il while costerebbe $O(m\log n)$.
• Il for scorre la lista di adiacenza di un nodo $y$. Tuttavia, ogni arco $(y,v)$ viene esaminato una sola volta in tutto l’algoritmo (quando il nodo $y$ viene estratto da $H$). Per ogni arco esaminato nel for, può essere eseguita un’operazione di inserimento in $H$, che ha costo $O(\log n)$. Poiché in totale ci sono $O(m)$ archi, il numero complessivo di operazioni di inserimento in $H$ è al massimo $O(m)$, e quindi il costo totale del for nell’intero algoritmo è $O(m\log n)$

La complessità di questa operazione è quindi $O(n\log n)+O(m\log n)+O(m\log n)=O((m+n)\log n)$