17 - B-tree

Il B-tree nasce dalla generalizzazione della struttura di file con indice.

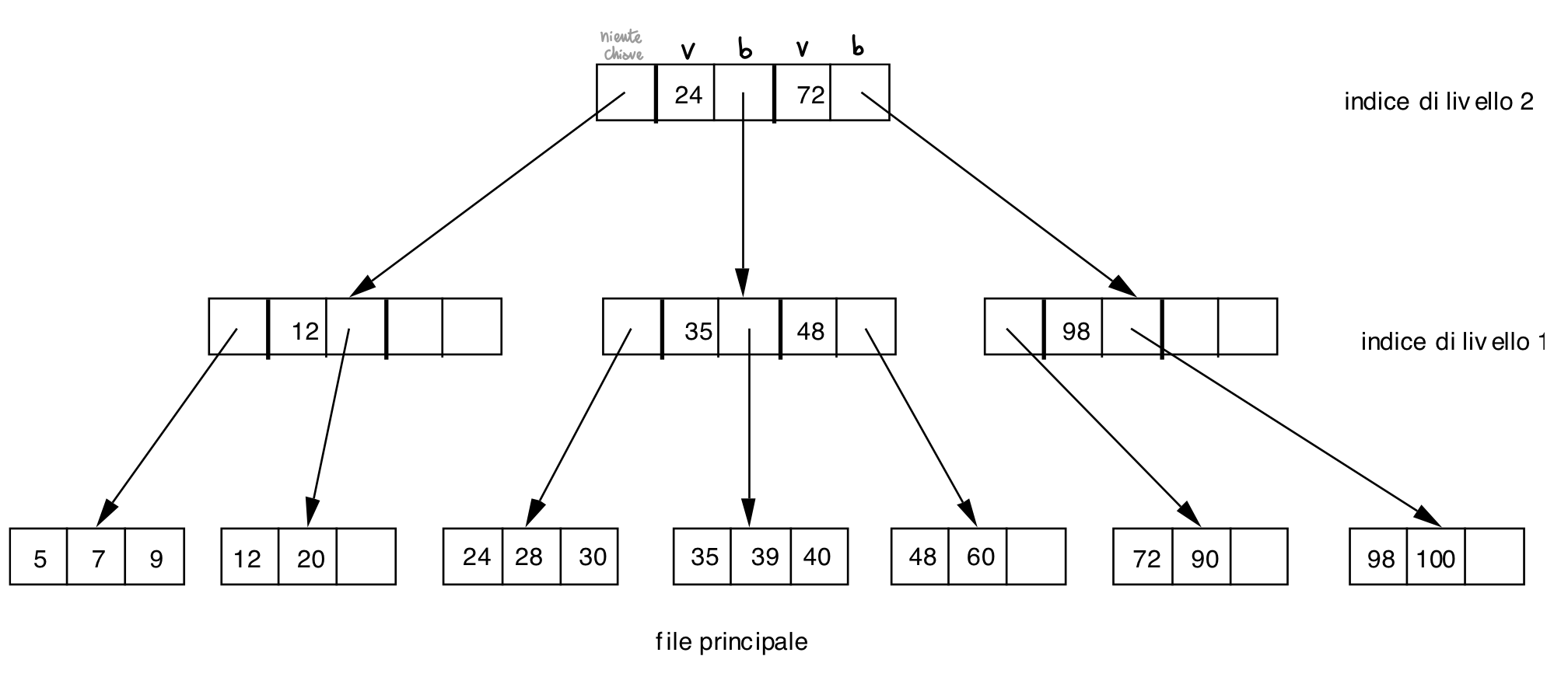
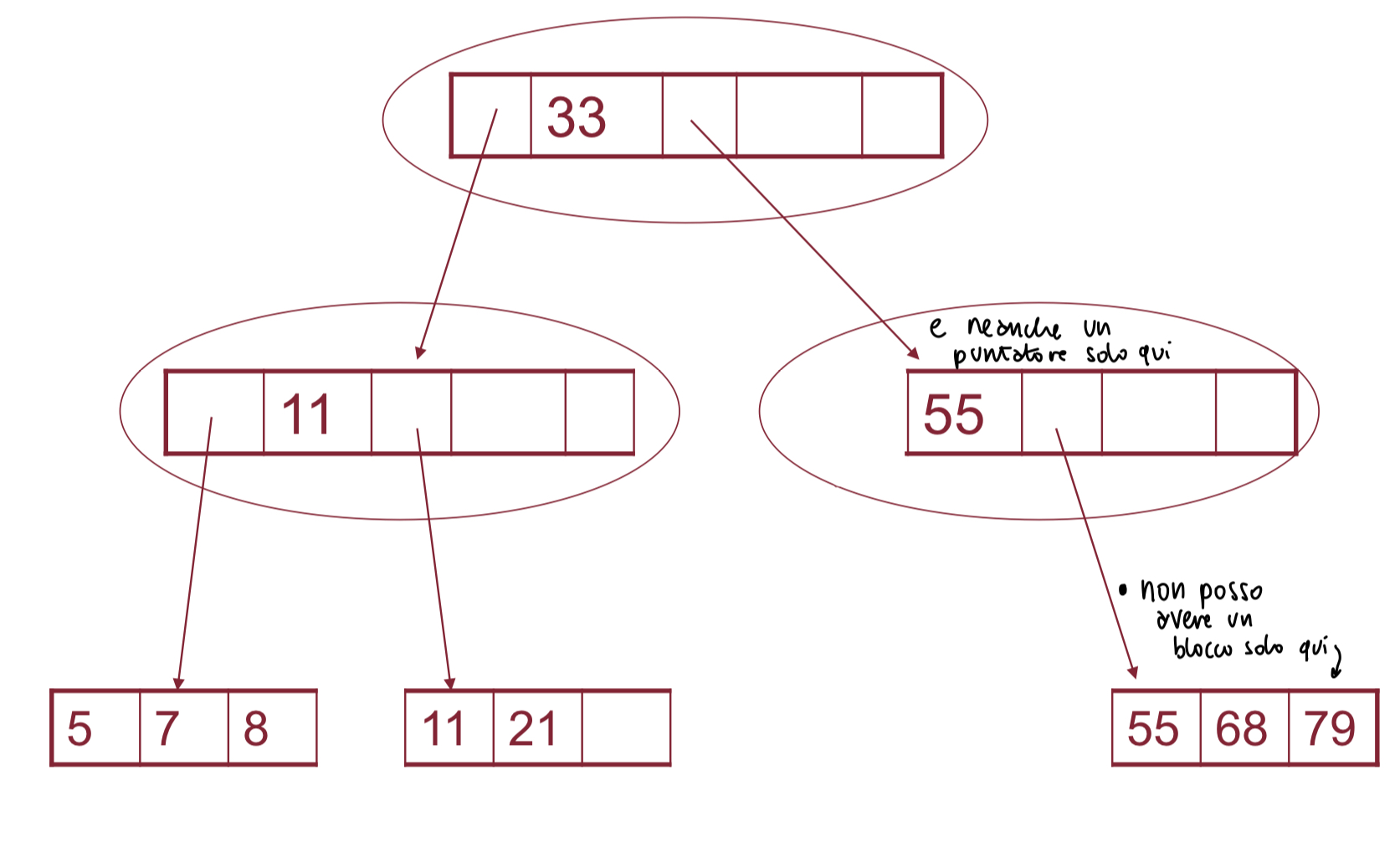
Si accede ad un file attraverso una gerarchia di indici - l’indice a livello più alto (radice) è costituito da un unico blocco e risiede in memoria principale. Ogni blocco di un file indice è costituito da record contenenti una coppia (v,b)

• v ⇒ valore della chiave del primo record della porzione del file principale a cui fa riferimento la coppia
• b ⇒ puntatore (ad un blocco del file indice a livello più basso, o ad un blocco del file principale)

il primo record indice di ogni blocco contiene solo un puntatore (niente chiave) ad un blocco che ha chiavi minori di quelle puntate dal secondo record

• ogni chiave di un record indice ricopre quelle del suo sottoalbero
• ogni blocco del file principale è memorizzato come quello di un ISAM

ogni blocco di un B-tree (sia indice che principale, tranne la radice) deve essere pieno almeno per metà

(per la radice, logicamente, il minimo è invece due record: se ce ne fosse uno solo, sarebbe inutile e la “vera” radice sarebbe quindi il blocco a cui il record punta)

ricerca

(per effettuare una ricerca, si accede agli indici a partire dal livello più alto: scendendo nella gerarchia degli indici, si restringe la porzione del file principale in cui deve trovarsi il record desiderato - fino ad arrivare ad un unico blocco).

Si parte dall’indice a livello più alto, e ad ogni passo si esamina un unico blocco (se è del file principale, deve essere quello - se è di un file indice, si cerca la chiave che ricopre la propria)

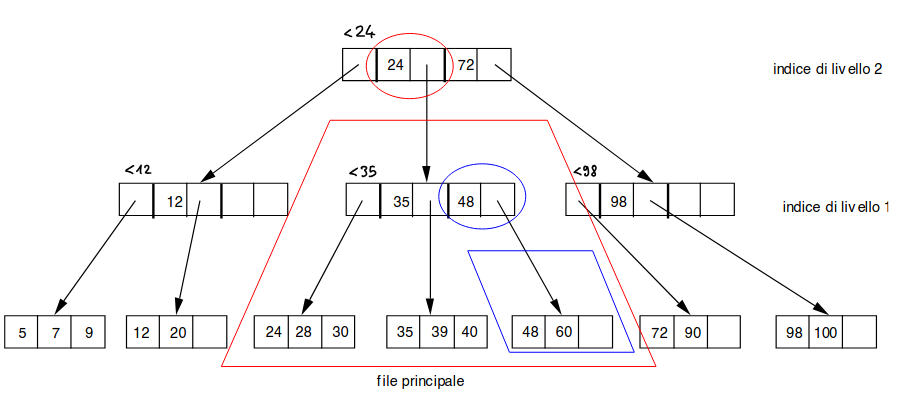
(per me è un po’ come il binary search tree ma n-ario) Il costo della ricerca - che è fisso, perché “so dove andare” - è di h+1 accessi (con h altezza dell’albero).

come varia h?

• più i blocchi sono pieni, più h è piccolo (meno costa la ricerca)
  • se i blocchi sono completamente pieni, un inserimento può richiedere una modifica dell’indice ad ogni livello

inserimento

L’inserimento ha costo h+1 (ricerca) + 1 (riscrivere il blocco) se c’è spazio sufficiente. Se non c’è spazio sufficiente, ha costo: h+1 (ricerca) + s (s⇐2h+1)

• nel caso peggiore, dobbiamo sdoppiare un blocco per ogni livello, effettuando due accessi in più + uno per la nuova radice

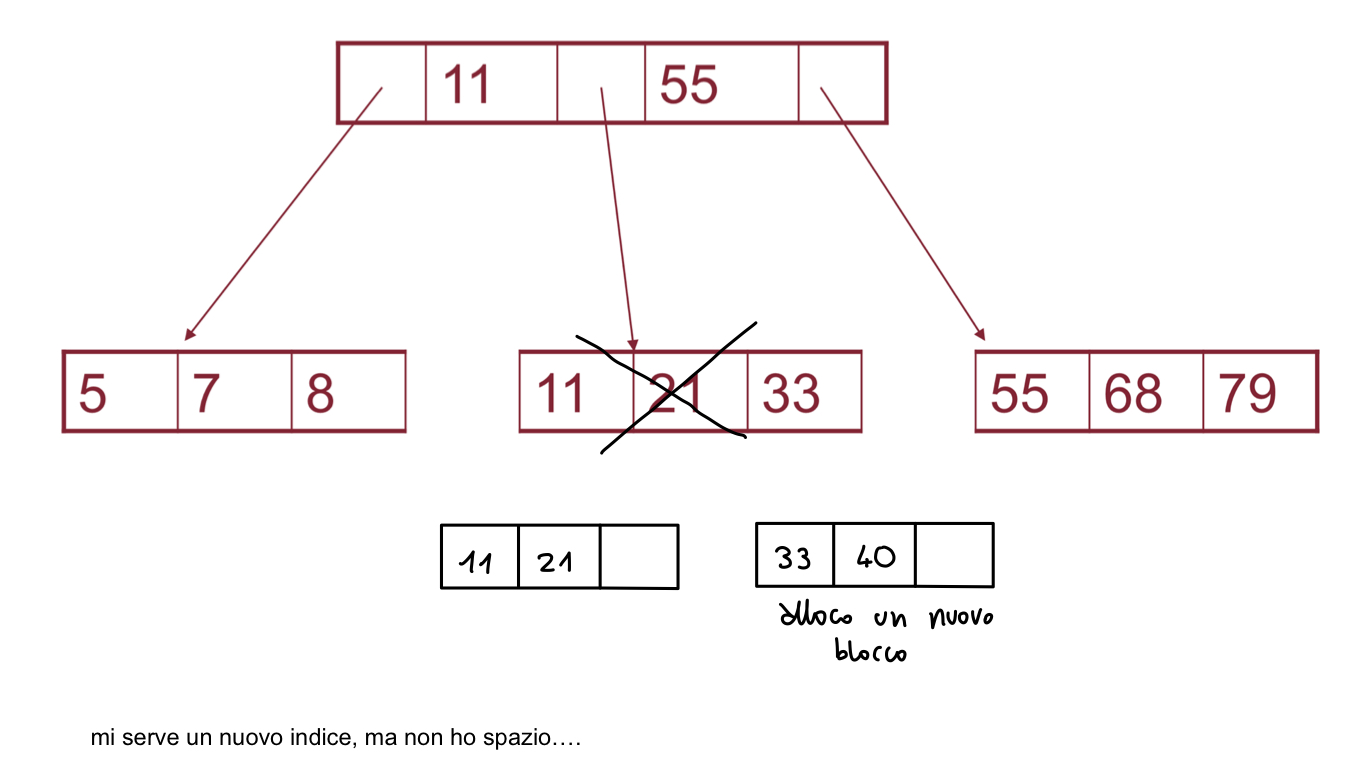
esempio

caso limite: voglio inserire un record, ma non ho spazio:

cancellazione

La cancellazione ha costo h+1 (ricerca) + 1 (riscrivere il blocco) se il blocco è pieno almeno per metà dopo la cancellazione. Altrimenti, sono necessari ulteriori accessi

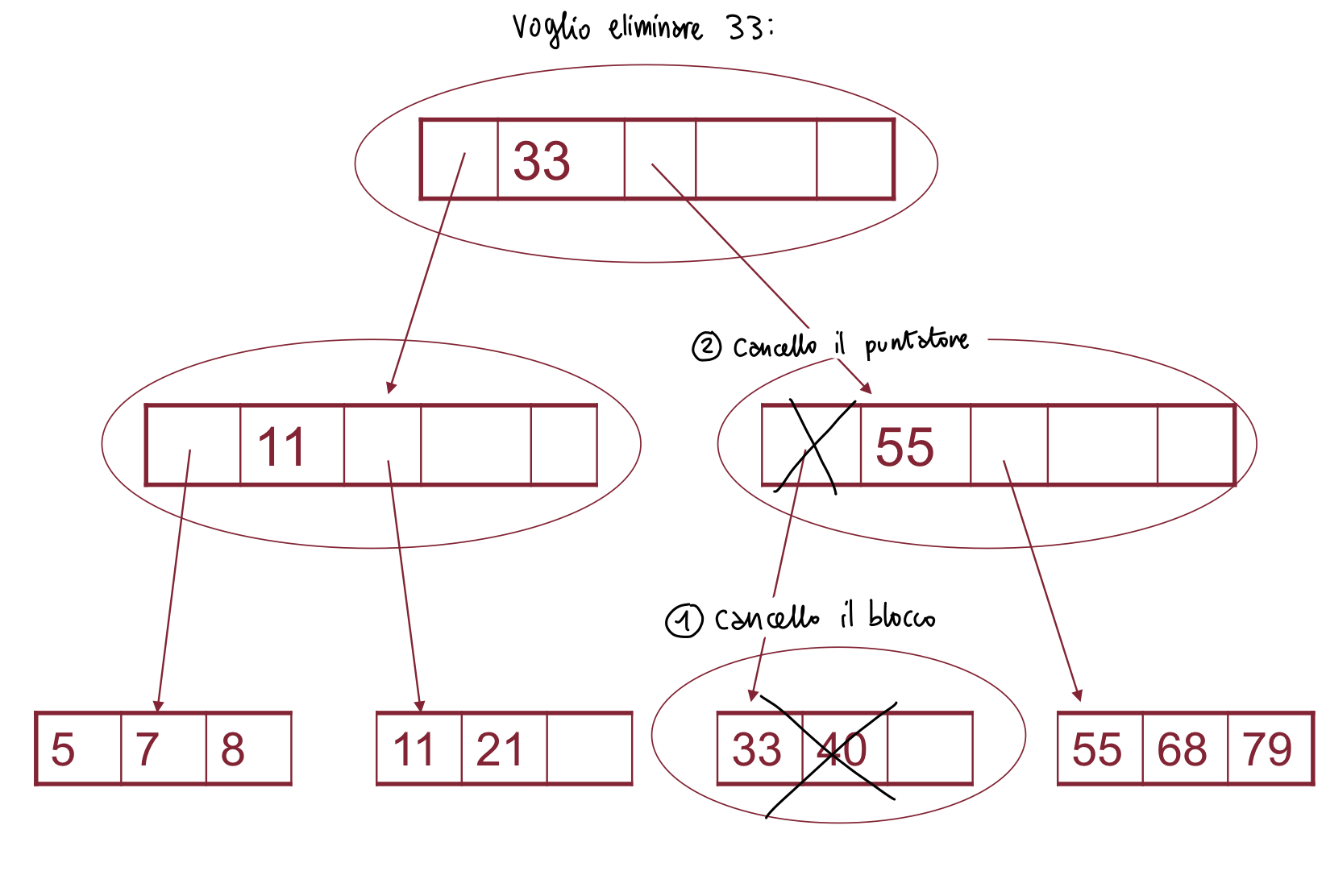
esempio

in alcuni casi, la cancellazione stravolge completamente la struttura dell’albero:

modifica

La modifica ha costo h+1 (ricerca) + 1 (riscrivere il blocco) se non coinvolge la chiave. Altrimenti, costo cancellazione + costo inserimento.

massimo valore di h

Siano:

• $N$ - numero di record nel file principale
• $2e-1$ - numero di reccord del file principale che possono essere memorizzati in un blocco
• $2d-1$ - numero di record del file indice che possono essere memorizzati in un bloicco

e quindi (poiché i blocchi devono essere riempiti a metà):

• $e$ - minimo di record necessari in ogni blocco del file principale
• $d$ - minimo di record necessari in ogni blocco del file indice

L’altezza massima ($k$) si ha quando i blocchi sono pieni al minimo, ovvero quando:

• ogni blocco del file principale contiene esattamente $e$ record
• ogni blocco del file indice contiene esattamente $d$ record

Quindi:

• il file principale ha al massimo $\frac{N}{e}$ blocchi (numero record/record x blocco)
• a livello $i$, il file indice ha
  • $\frac{N}{e{d}^{i-1}}$ record (ogni , memorizzati in:
  • $\frac{N}{e{d}^i}$ blocchi ($\frac{N}{e}$, che viene diviso per $d$ ad ogni livello)
    • (livello 1: $\frac{N}{ed}$ …)

A livello $k$, l’indice avrà esattamente un blocco, quindi dobbiamo fermarci quando: $\frac{N}{e{d}^k}=1⟺\frac{N}{e}=d^k⟺{\log }_d\left(\frac{N}{e}\right)=k$ (in realtà sarebbe $\lceil \frac{N}{e{d}^k}\rceil$, ma approssimiamo)

Quindi, il limite superiore dell’altezza dell’albero è ${\log }_d\left(\frac{N}{e}\right)$

esercizi

esercizio 1

Supponiamo di avere un file di $170.000$ record. Ogni record occupa $200$ byte, di cui $20$ per il campo chiave. Ogni blocco contiene $1024$ byte. Un puntatore a blocco occupa $4$ byte

• Se usiamo un B-tree e assumiamo che sia i blocchi indice che i blocchi del file sono pieni al minimo, quanti blocchi vengono usati per il livello foglia (file principale) e quanti per l’indice, considerando tutti i livelli foglia? Quale è il costo di una ricerca in questo caso?

Dati:

• il file contiene $170.000$ record ⇒ $NR=170.000$
• ogni record occupa $200$ byte ⇒ $R=200$
• il campo chiave occupa $20$ byte ⇒ $K=20$
• ogni blocco contiene $1024$ byte ⇒ $CB=1024$
• un puntatore a blocco occupa $4$ byte ⇒ $P=4$

Avremo: $MR=\lfloor \frac{CB}{R}\rfloor =\lfloor \frac{1024}{200}\rfloor =5$ con $MR$ massimo di record per blocco del file principale (byte per blocco/dimensione record)

Visto che sono pieni al minimo, divido per $2$ e prendo la parte intera per ottenere il numero di record effettivamente presenti (per blocco): $e=\lfloor \frac{5}{2}\rfloor =3$

Calcolo il numero di blocchi per il file principale (che è anche il numero di record del file indice) $BF=\lceil \frac{NR}{e}\rceil =\lceil \frac{170.000}{3}\rceil =56667$ (numero di record/record per blocco)

non per forza necessario

Possiamo calcolare il numero (massimo) dei blocchi in un file indice facendo: $\lfloor \frac{1024-4}{24}+1\rfloor \text{ ovvero }\frac{CB}{\text{dim. record (chiave+puntatore)}}$ (sottraggo 4 inizialmente perché il primo record non ha la chiave (quindi elimino lo spazio che il suo puntatore occupa), ma riaggiungo 1 al conto totale dei record perché è presente).

Calcoliamo il numero effettivo di record memorizzabili in un blocco del file indice. Il blocco è a metà capienza, quindi, invece di $1024$, useremo $512$

$d=\lceil \frac{CB/2-P}{K+P}\rceil +1=\lceil \frac{512-4}{24}\rceil +1=22+1=23$

verifica

per questo tipo di calcoli, è sempre utile fare una verifica, facendo il calcolo al contrario (verifichiamo effettivamente di aver occupato metà dei blocchi): $\text{risultato senza il primo puntatore}\cdot P+K⟺22\cdot 24+4=532$ okay, $532$ è più della metà - ma dobbiamo anche controllare che non sia troppo: proviamo a vedere cosa sarebbe successo con un record in meno $21\cdot 24+4=508$ $508<512$, quindi non saremmo arrivati a metà - il nostro risultato è corretto.

Calcoliamo il numero di blocchi per il file principale:

$FP=\lceil \frac{NR}{e}\rceil =\lceil \frac{170000}{3}\rceil =2464$
Calcoliamo il numero di blocchi per il file indice al primo livello

$B_1=\lceil \frac{BR}{d}\rceil =\lceil \frac{56667}{23}\rceil =2464$

Calcoliamo il numero di blocchi per il file indice al secondo livello

$B_2=\lceil \frac{B_1}{d}\rceil =\lceil \frac{2464}{23}\rceil =108$

Calcoliamo il numero di blocchi per il file indice al terzo livello

$B_3=\lceil \frac{B_2}{d}\rceil =\lceil \frac{108}{23}\rceil =5$

Calcoliamo il numero di blocchi per il file indice al quarto livello

$B_4=\lceil \frac{B_3}{d}\rceil =\lceil \frac{5}{23}\rceil =1$

A questo punto mi fermo poiché ho trovato la radice (livello con un solo blocco)

Complessivamente quindi si avranno $BI=B_1+B_2+B_3+B_4=2464+108+5+1=2578$ blocchi.

Il costo della ricerca sarà $5$ (un blocco per ognuno dei $4$ livelli di indice $+1$ blocco per il file principale)

domande orale

possibili domande orale

• struttura B-tree
• costo operazioni
• quando ha altezza massima? quant’è l’altezza massima?
• qual è l’unico blocco che non deve necessariamente essere pieno a metà?