11 - algoritmo di Bellman-Ford

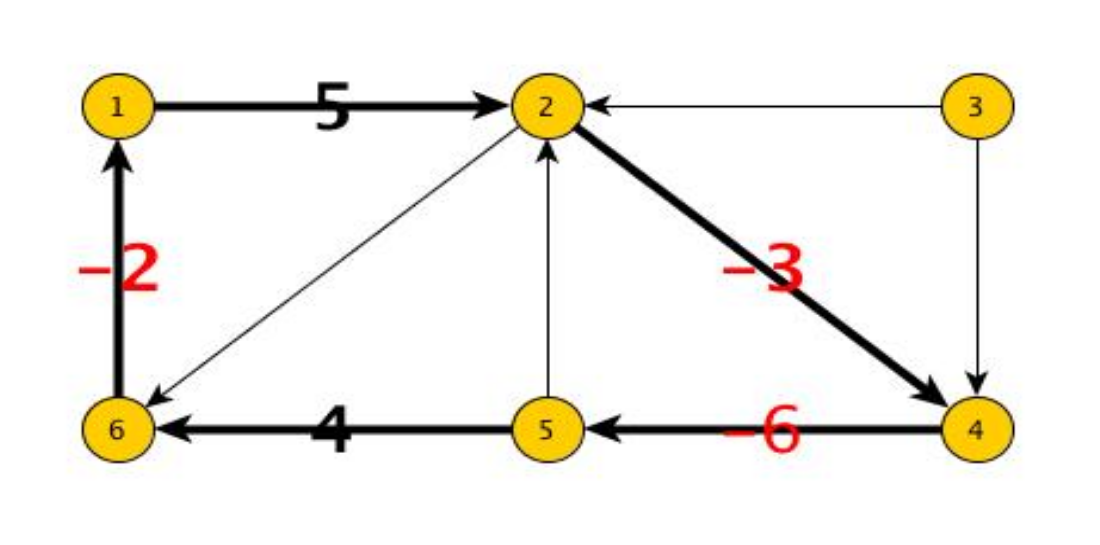
introduzione

Dato un grafo diretto e pesato $G$ in cui i pesi degli archi possono essere anche negativi e fissato un suo nodo $s$, si vuole determinare il costo minimo dei cammini che conducono da $s$ a tutti gli altri nodi del grafo.

• se non esiste un cammino, il costo sarà considerato infinito.

ciclo negativo

Un ciclo negativo è un ciclo diretto in un grafo la cui somma dei pesi degli archi è negativa.

se in un cammino tra i nodi $s$ e $t$ è presente un nodo che appartiene ad un ciclo negativo, allora non esiste un cammino di costo minimo tra $s$ e $t$.

Infatti, ripassando più volte per il ciclo, si abbasserebbe arbitrariamente il costo del cammino.

proprietà

Se il grafo $G$ non contiene cicli negativi, allora per ogni nodo $t$ raggiungibile dalla sorgente $s$ esiste un cammino di costo minimo che attraversa al più $n-1$ archi.

• infatti, se un cammino avesse più di $n-1$ archi, almeno un nodo verrebbe ripetuto formando un ciclo (e, visto che il grafo non ha cicli negativi, rimuovere cicli dal cammino non aumenterà il suo costo complessivo, quindi esisterà sempre un cammino ottimale di lunghezza $n-1$)

L’algoritmo di Bellman-Ford risolve il problema dei cammini di costo minimo in $O(n^2+m\cdot n)$.

Esso definisce la seguente tabella di dimensione $n\times n$:

• $T[i][j]=$ costo di un cammino minimo da $s$ al nodo $j$ di lunghezza al più $i$

Si costruisce la soluzione al problema determinando i valori delle righe della tabella.

• la soluzione sarà data dagli $n$ valori che si troveranno nell’ultima riga:

$\text{T[n-1][0], T[n-1][1], T[n-1][2], … T[n-1][n-1]}$

(il costo minimo per andare da $s$ al generico nodo $t$ sarà $T[n-1][t]$)

distanza di $s$ da se stesso

I valori della prima riga della tabella saranno tutti $+\infty$ tranne $T[0][s]$, che varrà $0$.

• si avrà anche che $T[i][s]=0\forall i>0$ (chiaramente il costo di un cammino da $s$ a $s$ sarà sempre $0$)

Per definire la regola che permette di calcolare i valori delle celle $T[i][j]$ con $j\ne s$ della riga $i>0$, bisogna distinguere due casi:

1. il cammino di lunghezza al più $i$ da $s$ ha lunghezza esattamente $i$
   • $T[i][j]=T[i-1][j]$
2. il cammino di lunghezza al più $i$ da $s$ ha lunghezza inferiore a $i$
   • ci troviamo nel caso in cui esiste un cammino minimo di lunghezza al più $i-1$ ad un nodo $x$ e un arco $(x,j)$
   • si prende, tra tutti gli archi che portano a $j$, quello che costa di meno, e si somma il suo costo al percorso che portava a $x$ (che si trova nella riga precedente)
   • $T[i][j]=mi{n}_{(x,j)\in E}(T[i-1][x]+costo(x,j))$

La formula che include entrambi i casi è:

$$\text{T[i][j]=}\left({\text{min(T[i−1][j]), min}}_{(x,j)\in E}\right(\text{T[i-1][x] + costo}(x,j)\left)\right)$$

formula per tutte le righe

$T[i][j]=\{\begin{array}{ll}0& \text{se }j=s\\ +\infty & \text{se }i=0\\ \left({\text{min(T[i−1][j]), min}}_{(x,j)\in E}\right(\text{T[i-1][x] + costo}(x,j)\left)\right)& \text{altrimenti}\end{array}$

implementazione

implementazione più efficiente: grafo trasposto

poiché nel calcolo della formula è necessario più volte conoscere gli archi entranti nel generico nodo $x$, conviene usare il grafo trasposto $G^T$ di $G$.

def Trasposto(G):
	n = len(G)
	GT = [ [] for _ in G]
	for i in range(n):
		for j, costo in G[i]:
			GT[j].append((i, costo))
	return GT
 
def CostoCammini(G, s):
	n = len(G)
	inf = float('inf')
	T = [ [inf]*n for _ in range(n)]
	T[0][s] = 0
	GT = Trasposto(G)
	
	for i in range(1, n): # righe della matrice
		for j in range(n): # nodi per ogni riga
			T[i][j] = T[i-1][j]	
			for x, costo in GT[j]:
				T[i][j] = min(T[i][j], T[i-1][x] + costo)
	return T[n-1]

• l’inizializzazione della tabella $T$ costa $\Theta (n^2)$
• la costruzione di $G^T$ costa $O(n+m)$
• i tre for annidati non hanno limite superiore non $O(n^3)$ (come potrebbe sembrare), perché:
  • i due for più interni hanno costo totale $\Theta (m)$ (scorrono tutte le liste di adiacenza in $G^T$ - infatti, se nel primo for si itera su tutti i nodi, non si entrerà nel secondo perché non ci saranno archi entranti)

La complessità totale è quindi $O(n^2+n\cdot m)$

ottimizzazioni

1. Se la riga $k$ della tabella $T$ è uguale alla riga $k-1$, anche le righe successive non varieranno: in questo caso, conviene terminare l’algoritmo senza calcolare le righe restanti.

• questo accorgimento non migliora il costo asintotico dell’algoritmo ma può fare differenza nella pratica

2. Non serve memorizzare l’intera tabella $T$: bastano le ultime due righe. L’algoritmo può essere facilmente modificato per utilizzare memoria $O(n)$ e non $O(n^2)$

trovare cicli negativi

Una piccola modifica all’algoritmo permette di scoprire se il grafo contiene cicli negativi raggiungibili da $s$.

• basta infatti calcolare una riga in più della tabella (quindi la riga $n$) con il costo dei cammini minimi di lunghezza al più $n$
• se le righe $n$ e $n-1$ risultano diverse, allora nel grafo è presente un ciclo negativo

trovare i cammini

Oltre al costo dei cammini, è possibile usare Bellman-Ford per costruire l’albero $P$ dei cammini minimi.

• basta mantenere, per ogni nodo $j$, il suo predecessore: il nodo $u$ che lo precede nel cammino
• il valore di $P[j]$ verrà aggiornato ogni volta che il valore $T[i][j]$ cambia (ovvero diminuisce) perché è stato trovato un cammino migliore

def costo_cammini1(G, s):
	T = [[float('inf')]*len(G) for _ in range(len(G))]
	P = [-1]*len(G)
	GT = trasposto(G)
	
	T[0][s] = 0
	P[s] = s
	for i in range(1,n)
		for j in range(n):
			if j==s:
				T[k][j] = 0
			else:
				for x,costo in GT[j]:
					if T[k-1][x]+costo < T[k][j]:
						T[k][j] = T[k-1][x]+costo
						P[j] = x
						# ^ l'attuale cammino minimo
						# che arriva a j lo fa tramite x
	return T[len(G)-1], P

Al termine dell’algoritmo:

• $\text{T[n-1][j]}\ne \infty$ ⇒ $j$ è raggiungibile da $s$
  • $P[j]$ conterrà il nodo che precede $j$ nel cammino minimo da $s$ a $j$
• $\text{T[n-1][j]}=\infty$ ⇒ $j$ non è raggiungibile da $s$
  • $P[j]$ conterrà -1