11 - decomposizioni che hanno un join senza perdita

Se si decompone uno schema di relazione $R$, si vuole che la decomposizione ottenuta sia tale che che ogni istanza legale $r$ di $R$ sia ricostruibile mediante join naturale da un’istanza legale $\{r_1,r_2,\dots ,r_k\}$ dello schema decomposto $\{R_1,R_2,\dots ,R_k\}$.

definizione

Sia $R$ uno schema di relazione. Una decomposizione $\rho =\{R_1,R_2,\dots ,R_k\}$ di $R$ ha un join senza perdita se per ogni istanza legale di $r$ si ha: $r={\pi }_{R_1}(r)\bowtie {\pi }_{R_2}\bowtie \cdots \bowtie {\pi }_{R_k}(r)$

introduciamo $m_p(r)$

definiamo $m_{\rho }(r)={\pi }_{R_1}(r)\bowtie {\pi }_{R_2}\bowtie \cdots \bowtie {\pi }_{R_k}(r)$

join naturale delle proiezioni dei sottoschemi su $r$ (che deve quindi essere uguale a $r$ stessa)

in pratica

Dato uno schema $R=A_1{A}_2{A}_3\dots An$, un sottoschema $R_i$ è un suo sottoinsieme (es. $A_1{A}_2{A}_3$). La proiezione ${\pi }_{R_i}(r)$ di un’istanza legale $r$ su un sottoschema $R_i$ prende ogni tupla di $r$ e mantiene solo gli attributi che appartengono a $R_i$.

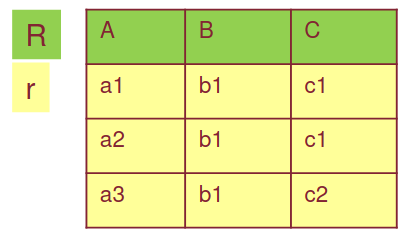
Per esempio, se ho $R=ABC$ con le dipendenze funzionali $F=\{A\to B,C\to B\}$ con quest’istanza legale $r$:

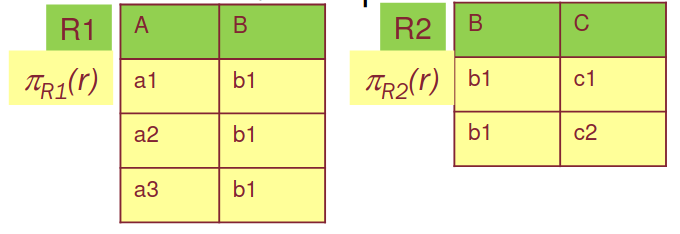
Con i sottoschemi $R_1=AB$, $R_2=BC$, $r$ si decompone in:

(le tuple manterranno solo gli attributi di $R_i$)

(nella proiezione su $R_2$, si “perde” una tupla perché risulta duplicata).

In questo caso, effettuando il join delle due decomposizioni, non otteniamo l’istanza legale di partenza:

teorema

Sia $R$ uno schema di relazioni e $\rho =R_1,R_2,\dots ,R_k$. Per ogni istanza legale $r$ di $R$ e per il “suo” $m_{\rho }$ si ha:

1. $r\subseteq m_{\rho }(r)$ - non serve dimostrarlo perché $m_{\rho }(r)$ non potrà mai contenere istanze in meno, quindi al minimo è $=r$
2. ${\pi }_{R_i}(m_{\rho })={\pi }_{R_i}(r)$
   • ${\pi }_{R_i}(r)\subseteq {\pi }_{R_i}(m_{\rho })$ deriva da (1)
   • ${\pi }_{R_i}(r)\supseteq {\pi }_{R_i}(m_{\rho })$: per ogni tupla $t\in m_{\rho }(r)$ ne esiste un’altra $t^{\prime }\in r$ tale che $t[R_i]=t^{\prime }[R_i]$ (altrimenti non avremmo $t[R_i]$ in ${\pi }_{R_i}(r)$ e quindi nel join)
3. $m_{\rho }(m_{\rho }(r))=m_{\rho }(r)$

(dimostrazioni non richieste per l’orale)

verifica

esiste un algoritmo che permette di verificare se una decomposizione data ha un join senza perdita in tempo polinomiale:

• input: uno schema di relazione $R$, un insieme $F$ di dipendenze funzionali su $R$, una decomposizione $\rho =\{R_1,R_2,\dots ,R_3\}$
• output: decide se $\rho$ ha un join senza perdita

$$\begin{array}{rl}& \mathbf{begin}\\ & \text{Costruisci una tabella }r\text{ nel modo seguente:}\\ & r\text{ ha }\#R\text{ colonne e }\#\rho \text{ righe}\\ & \text{all’incrocio dell’i-esima riga e della j-esima colonna metti}\\ & \text{il simbolo }{a}_j\text{ se l’attributo }{A}_j\in R_i\\ & \text{il simbolo }{b}_{ij}\text{ altrimenti}\\ & \mathbf{repeat}\\ & \mathbf{for}\mathbf{every}\mathbf{X}\to \mathbf{Y}\in \mathbf{F}\\ & \mathbf{do}\mathbf{if}\text{ ci sono due tuple }{t}_1\text{ e }{t}_2\text{ in }r\text{ tali che }{t}_1[X]=t_2[X]\text{ e }{t}_1[Y]\ne t_2[Y]\\ & \mathbf{then}\mathbf{for}\mathbf{every}\mathbf{attribute}{\mathbf{A}}_{\mathbf{j}}\in \mathbf{Y}\\ & \mathbf{do}\mathbf{if}{t}_1[A_j]{=}^{\prime }{a_j}^{\prime }\\ & \mathbf{then}{t}_2[A_j]:=t_1[A_j]\\ & \mathbf{else}{t}_1[A_j]:=t_2[A_j]\\ & \mathbf{until}r\text{ ha una riga con tutte ’a’ }\mathbf{or}r\text{ non eˋ cambiato}\\ & \mathbf{if}r\text{ ha una riga con tutte ’a’}\\ & \mathbf{then}\rho \text{ ha un join senza perdita}\\ & \mathbf{else}\rho \text{ non ha un join senza perdita}\end{array}$$

quando finisce l’algoritmo, o:

• sono arrivato alla fine e non posso più cambiare cose (è un’istanza legale)
• mi fermo in anticipo - le a non possono diventare b, e ho trovato una tupla di tutte a (so già che l’istanza diventerà legale alla fine dell’algoritmo, e posso fermarmi perché non ho perdite)

spieghiamo meglio

• costruiamo una tabella $r$ in modo da evere un numero di colonne pari al numero di attributi in $R$ e un numero di righe pari al numero di sottoschemi nella decomposizione $\rho$
• nelle celle ad indice $i$ per le righe e $j$ per le colonne, inseriamo $a_j$ se l’attributo della colonna $j$ appartiene al sottoschema della riga $i$ - altrimenti inseriamo $b_{ij}$
• adesso, per ogni dipendenza $X\to Y\in F$, controlliamo se nella tabelle i sono tuple che non rispettano la dipendenza (ovvero $t_1[X]=t_2[X]$ e $t_1[Y]\ne t_2[Y]$) - le “facciamo diventare legali”: se in una tupla è presente una $a$ nell’attributo $Y$, la propaghiamo a tutte le altre, altrimenti scegliamo un $b$ a piacere e lo propaghiamo su tutte le altre (due attributi sono uguali se hanno entrambi $a$ o una $b$ con lo stesso pedice)

esempio

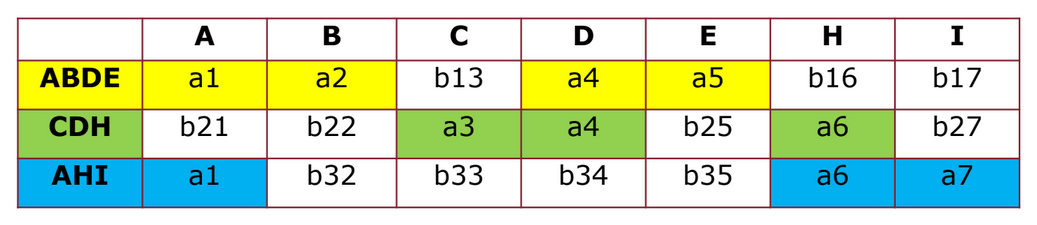
dati $R=(A,B,C,D)$ e $F=\{C\to D,AB\to E,D\to B\}$ dire se la decomposizione $\rho =\{AC,ADE,CDE,AD,B\}$ ha un join senza perdite

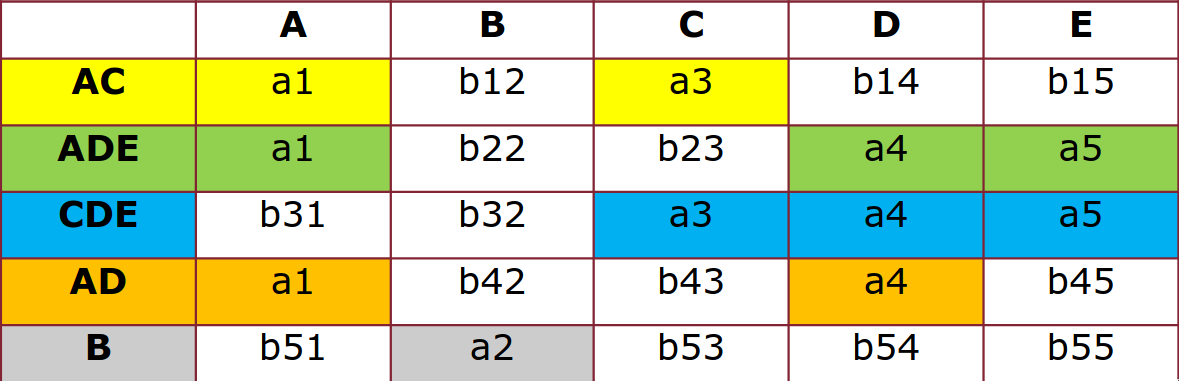
prima iterazione:

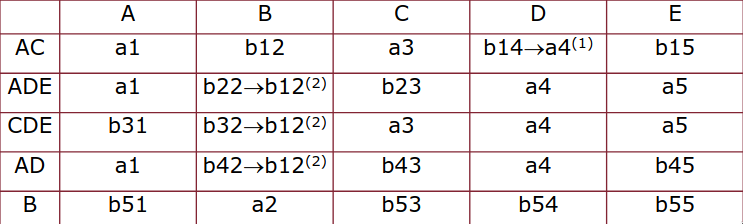
in ordine rispetto alle dipendenze funzionali:

• $C\to D$: la prima e la terza riga coincidono su $C=a3$ - cambiamo $b14$ in $a4$ in modo che la dipendenza funzionale sia soddisfatta
• $AB\to E$ è già soddisfatta
• $D\to B$: nelle prime quattro righe, $D=a4$, quindi cambiamo $b22$, $b32$, $b42$ in $b12$

seconda iterazione:

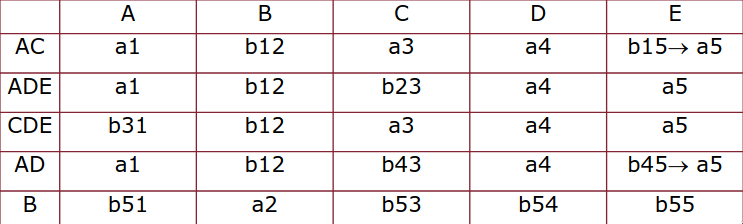
• $C\to D$ è già soddisfatta
• $AB\to E$: prima, seconda e quarta riga coincidono su $AB$, quindi cambiamo $b15$ e $b45$ in $a5$
• $D\to B$ è già soddisfatta

terza iterazione (fine):

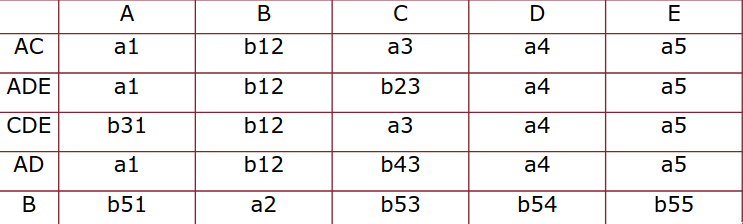
• non c’è più nulla da cambiare quindi l’algoritmo termina.

Bisogna verificare se c’è una tupla con tutte $a$ - non c’è, quindi il join non è senza perdita.

teorema

Sia $R$ uno schema di relazione, $F$ un insieme di dipendenze funzionali su $R$ e $\rho =\{R_1,R_2,\dots ,R_k\}$ una decomposizione di $R$. L’algoritmo di verifica decide correttamente se $\rho$ ha un join senza perdita.

dimostrazione

Occorre dimostrare che $\rho$ ha un join senza perdita (ovvero $m_{\rho }=r$ per ogni $r$ legale) $⟺$ quando l’algoritmo termina, la tabella ha una tupla con tutte ‘a’.

Si dimostra solo la parte “join senza perdita $⟹$ tupla con tutte ‘a’“.

Supponiamo per assurdo che $\rho$ abbia un join senza perdita $(m_{\rho }(r)=r)$ e che al termine dell’algoritmo la tabella $r$ non abbia una tupla con tutte ‘a’. La tabella $r$ (finale) può essere interpretata come un’istanza legale di $R$, in quanto al termine dell’algoritmo non ci sono violazioni di dipendenze in $F$.

La tabella $r$ iniziale contiene ‘a’ in ogni riga per gli attributi che appartengono al sottoschema a cui fa riferimento quella riga.

esempio:

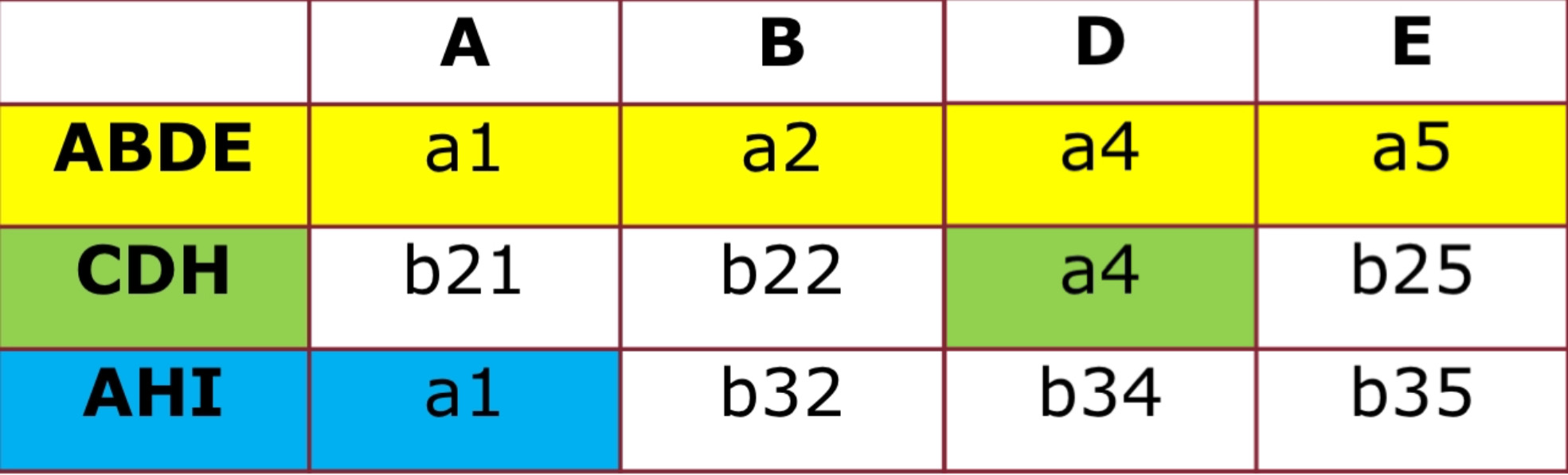
Quindi ogni proiezione ${\pi }_{R_i}(r)$ della tabella su un sottoschema avrà una tupla di tutte ‘a’ (la riga che corrisponde a $R_i$.)

per esempio, proiezione su $ABDE$:

Quando si fa il join naturale tra due proiezioni ${\pi }_{R_i}(r)$ ed ${\pi }_{R_j}(r)$ (con le loro tuple con tutte ‘a’ che chiamiamo $t_i$ e $t_j$), ci sono due casi:

• o $R_i$ e $R_j$ condividono (almeno) un attributo ⇒ sappiamo che $t_i$ e $t_j$ avranno lo stesso valore su quell’attributo (‘a’), e quindi saranno unite, formando un’unica tupla con tutte ‘a’
• o le due proiezioni non hanno attributi in comune ⇒ in questo caso il join naturale degenererà in prodotto cartesiano, e tutte le tuple di ${\pi }_{R_i}(r)$ e ${\pi }_{R_j}(r)$ saranno unite (quindi anche $t_i$ e $t_j$)

In entrambi casi, il join naturale ci porterà ad unire $t_i$ e $t_j$ e ad avere una tupla con tutte ‘a’.

Visto che $m_{\rho }(r)$ è il join naturale di tutte le proiezioni, esso contiene quindi sicuramente una tupla con tutte ‘a’. L’ipotesi di partenza, per cui abbiamo un join senza perdita ci impone che $m_{\rho }(r)=r$, contraddicendo quindi la supposizione per cui $r$ non ha tuple con tutte ‘a’.

Abbiamo quindi dimostrato che “join senza perdita $⟹$ tupla con tutte ‘a‘“.

domande orale

possibili domande orale

• come definiamo $m_{\rho }(r)$?
• quando una decomposizione ha join senza perdita?
• teorema su $m_{\rho }(r),r,{\pi }_{R_i}$
• dimostrazione join senza perdita $⟹$ riga con tutte a