15 - file hash

il file è suddiviso in bucket numerati da 0 a $B-1$.

• ciascun bucket è costituito da uno o più blocchi collegati tramite puntatori, ed è organizzato come un heap

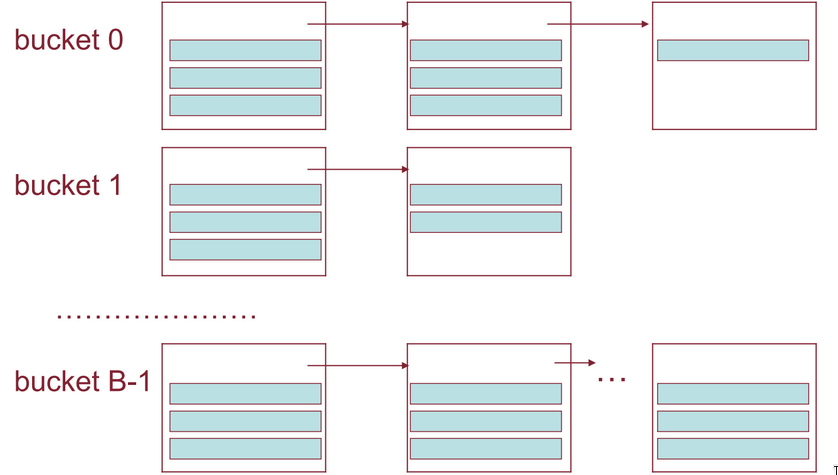
bucket directory

L’accesso ai bucket avviene attraverso la bucket directory, che contiene $B$ elementi. L’i-esimo puntatore contiene l’indirizzo (bucket header) del primo blocco dell’i-esimo bucket.

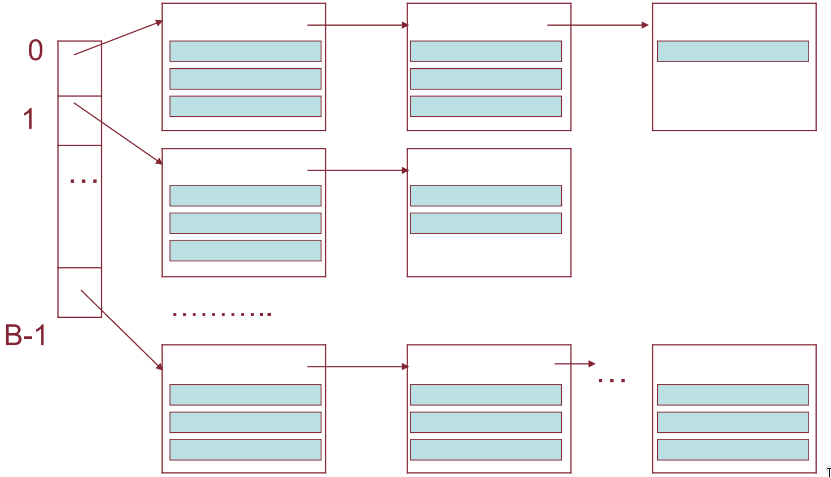
funzione hash

Il numero del bucket in cui deve trovarsi un record con chiave v è calcolato tramite una funzione hash h(v), che restituisce un valore da 0 a $B-1$ (sicuramente si userà quindi $\%B$)

operazioni

Una qualsiasi operazione su un file hash richiede:

• la valutazione di h(v) per individuare il bucket
• l’esecuzione dell’operazione sul bucket, che è organizzato come un heap

Poiché l’inserimento di un record viene effettuato sull’ultimo blocco del bucket (perché ogni bucket è una heap), è opportuno che la bucket directory contenga anche, per ogni bucket, un puntatore all’ultimo record del bucket.

costo operazioni

Se la funzione hash distribuisce uniformemente i record nei bucket, ogni bucket è costituito da $\frac{n}{B}$ blocchi, e quindi

• il costo richiesto di un’operazione è approssimativamente 1/B-esimo del costo dell’operazione se il file fosse organizzato come una heap

funzione hash

Una buona funzione hash deve ripartire uniformemente i record nei bucket, cioè, al variare della chiave, deve assumere con la stessa probabilità uno dei valori compresi tra 0 e B-1.

In genere, una funzione hash trasforma la chiave in un intero, lo divide per B e usa il resto della divisione come numero del bucket in cui deve trovarsi il record.

considerazioni

Appare evidente che quanti più sono i bucket, tanto più è basso il costo di un’operazione. Ma il numero di bucket è limitato dalle seguenti considerazioni:

• ogni bucket deve avere almeno un blocco
• conviene che la bucket directory sia contenuta in memoria principale, o saranno necessari ulteriori accessi per leggere il suo contenuto

esempi

esempio 1

abbiamo i seguenti dati:

• il file contiene 250.000 record ⇒ $NR=250.000$
• ogni record occupa 300 byte ⇒ $R=300$
• il campo chiave occupa 75 byte (“trappola” - è un dato inutile per questo tipo di organizzazione) ⇒ $K=75$
• ogni blocco contiene 1024 byte ⇒ $CB=1024$
• un puntatore a un blocco occupa 4 byte ⇒ $P=4$

a) Se usiamo un’organizzazione hash con 1200 bucket ($B=1200$), quanti blocchi occorrono per la bucket directory ?

Indichiamo con $B$ il numero di bucket e con $BD$ il numero di blocchi per la bucket directory (array di puntatori indicizzato da $0$ a $B-1$).

1. quanti puntatori entrano in un blocco?

$PB=\lfloor \frac{CB}{P}\rfloor$ (dimensione blocco/dimensione puntatore) - parte intera inferiore perché devono essere contenuti interamente $PB=\frac{1024}{4}=256$

2. quanti blocchi ci servono per la bucket directory? e per il file hash?

$BD=\lceil \frac{B}{PB}\rceil =\lceil \frac{1200}{256}\rceil =\lceil 4,69\rceil =5$ - parte superiore perché i blocchi vengono allocati interamente

b) Quanti blocchi occorrono per i bucket, assumendo una distribuzione uniforme dei record nei bucket?

supponiamo di non avere un direttorio di record all’inizio del blocco (e quindi che tutto lo spazio sia occupato dai dati). serve però un puntatore per ogni blocco per linkare i blocchi dello stesso bucket.

In un blocco dobbiamo quindi memorizzare il maggior numero possibile di record + un puntatore per un eventuale prossimo blocco nel bucket. Abbiamo due modi per calcolare il massimo numero di record per blocco:

1. Sappiamo che $M\cdot R+P\le CB$ , ovvero il massimo numero di record x la dimensione di un record con aggiunto il puntatore deve essere minore o uguale della dimensione di un blocco (sono tutte le informazioni che inseriamo in un blocco) Quindi, $M\le \frac{1020}{300}=3,4$. Sappiamo che $M$ deve essere intero (i record non possono stare a cavallo), quindi possiamo assumere $M=3$

2. possiamo anche sottrarre la taglia del puntatore dallo spazio utilizzabile in un blocco e prendere la parte intera inferiore della divisione dello spazio rimanente per la taglia dei record - $M=\lfloor \frac{CB-P}{R}\rfloor =\lfloor \frac{1020}{300}\rfloor =3$

se il blocco ha un puntatore al blocco precedente $P$ nella diseguaglianza)

in questo caso devo sottrarre lo spazio di un altro puntatore da quello disponibile (o moltiplicare per due

Se la distribuzione dei record nei bucket è uniforme, avremo $RB=\lceil \frac{NR}{B}\rceil$ ovvero numero di record in un bucket = $\frac{\text{numero di record}}{\text{numero di bucket}}$

Occorrono quindi $NB=\lceil \frac{RB}{M}\rceil =\lceil \frac{209}{3}\rceil =70$ blocchi per bucket (ho $RB$ record “totali” in un bucket da distribuire in diversi blocchi)

Per trovare il numero di blocchi necessario per il file hash, basta moltiplicare il numero di blocchi necessari per un bucket per il numero di bucket: $BB=NB\times B=70\times 1200=8400$

3. qual è il costo medio della ricerca?

Se la distribuzione è uniforme, visto che la ricerca avviene solo sul bucket individuato dalla fuzione hash, (avremo un numero di accessi pari a quello che si avrebbe su un heap della stessa dimensione del bucket) accederemo in media alla metà dei blocchi di un bucket. Avremo quindi $MA=\lceil \frac{NB}{2}\rceil =\lceil \frac{70}{2}\rceil =35$

4. quanti bucket dovremmo creare per avere un numero medio di accessi a blocco ⇐ 10, assumendo comunque una distribuzione uniforme?

Dobbiamo riscrivere l’espressione di $MA$ in modo che compaia esplicitamente il numero di bucket $B$ (tralasciando gli arrotondamenti). Avremo quindi $MA=\lceil \frac{NB}{2}\rceil =\lceil \frac{\left(\frac{RB}{M}\right)}{2}\rceil =\lceil \frac{\frac{\left(\frac{NR}{B}\right)}{M}}{2}\rceil =\lceil \frac{NR}{2(B\times M)}\rceil$. Dobbiamo calcolare $B$ in modo tale che $\lceil \frac{NR}{2(B\times M)}\rceil \le 10$, ovvero $B\ge \frac{NR}{20M}$. Nel nostro caso, avremmo $B\ge \frac{250000}{(20\times 3)}=4167$.

Si può anche ragionare in un altro modo: sappiamo che $MA=\lceil \frac{NB}{2}\rceil$, quindi, per avere $MA\le 10$, dobbiamo avere $NB\ge 20$ (con $NB$ numero di blocchi in un bucket). Quindi, dobbiamo avere $RB=M\times NB\le M\times 20$, quindi $RB\le 60$. Perché sia possibile, serve $\frac{NR}{B}\le 60$ e quindi $B\ge \frac{250000}{60}$

domande orale

possibili domande orale

• struttura file hash
• cosa deve fare una “buona” funzione hash?
• costo delle operazioni su un file hash