6 - chiusura di un insieme di dipendenze funzionali

(due insiemi che hanno la stessa chiusura avranno le stesse istanze legali - perché la chiusura è l’insieme di dipendenze che viene soddisfatto da ogni istanza legale)

$F\subseteq F^{+}=G^{+}\supseteq G$ non vuol dire che $F=G$, ma che i due hanno le stesse istanze legali (posso scambiarli).

assiomi di Armstrong

Denotiamo come $F^A$ l’insieme di dipendenze funzionali definito nel modo seguente:

• $\text{se }f\in F\text{ allora }f\in F^A$
• se rispetta l’assioma della riflessività
• se rispetta l’assioma dell’aumento
• se rispetta l’assioma della transitività

Dimostreremo che $F^{+}=F^A$, ovvero che la chiusura di un insieme di dipendenze funzionali F ($F^{+}$) $può essere ottenuta a partire da F applicando ricorsivamente i tre assiomi di Armstrong.

assioma della riflessività

$\text{se }Y\subseteq X\subseteq R\text{ allora }X\to Y\in F^A$

esempio

$\text{Nome}\subseteq (\text{Nome, Cognome})$

• ovviamente se due tuple hanno uguale la coppia $(\text{Nome, Cognome})$ allora sicuramente avranno uguale l’attributo $\text{Nome}$ (e $\text{Cognome}$), quindi
• $(\text{Nome, Cognome})\to \text{Nome}$ viene sempre soddisfatta

assioma dell’aumento

$\text{se }X\to Y\in F^A\text{ allora }XZ\to YZ\in F^A\forall Z\subseteq R$

esempio

• $\text{CodFiscale}\to \text{Cognome}$ è soddisfatta quando, se due tuple hanno $\text{CodFiscale}$ uguale, allora hanno anche $\text{Cognome}$ uguale.
• Se aggiungo l’attributo $\text{Indirizzo}$, avrò che se due tuple sono uguali su $(\text{CodFiscale, Indirizzo})$ lo devono essere anche su $(\text{Cognome, Indirizzo})$
• Quindi se viene soddisfatta $\text{CodFiscale}\to \text{Cognome}$ viene soddisfatta anche $\text{CodFiscale, Indirizzo}\to \text{Cognome, Indirizzo}$

assioma della transitività

$\text{se}X\to Y\in F^A\text{ e }Y\to Z\in F^A\text{ allora }X\to Z\in F^A$

esempio

• $\text{Matricola}\to \text{CodFiscale}$ è soddisfatta quando, se due tuple hanno $\text{Matricola}$ uguale, allora hanno anche $\text{CodFiscale}$ uguale.

• $\text{CodFiscale}\to \text{Cognome}$ è soddisfatta quando, se due tuple hanno $\text{CodFiscale}$ uguale, allora hanno anche $\text{Cognome}$ uguale.

• Allora se entrambe le dipendenze sono soddisfatte, e due tuple hanno $\text{Matricola}$ uguale, allora hanno anche $\text{CodFiscale}$ uguale, ma questo implica che hanno anche $\text{Cognome}$ uguale.

• Quindi se entrambe le dipendenze sono soddisfatte, ogni volta che due tuple hanno $\text{Matricola}$ uguale avranno anche $\text{Cognome}$ uguale, e quindi viene soddisfatta anche $\text{Matricola}\to \text{Cognome}$

  ($\text{Matricola}\to \text{CodFiscale}\to \text{Cognome}$)

conseguenze degli assiomi di Armstrong

Ci sono altre tre regole che producono elementi di $F^A$.

regola dell’unione

$$\text{se }X\to Y\in F^A\text{ e }X\to Z\in F^A\text{ allora }X\to YZ\in F^A$$

esempio

• Se $\text{CF}\to \text{Nome}$
• e $\text{(Nome, Cognome)}\to \text{(Nome, Padre)}$
• allora $\text{(CF, Cognome)}\to \text{(Nome, Padre)}$

dimostrazione

• Se $X\to Y\in F^A$, per l’assioma dell’aumento si ha $X\to XY\in F^A$ (sono insiemi, $\text{XX=X}$)
• Analogamente se $X\to Z\in F^A$, per l’assioma dell’aumento si ha $XY\to YZ\in F^A$
• Quindi poiché $X\to XY\in F^A$ e $XY\to YZ\in F^A$, per l’assioma della transitività si ha $X\to YZ\in F^A$

regola della decomposizione

$\text{se }X\to Y\in F^A\text{ e }Z\subseteq Y\text{ allora }X\to Z\in F^A$ $\text{(X}\to \text{sottoinsiemi di Y)}$

esempio

• Se $\text{CF}\to \text{(Nome, Cognome)}$
• (chiaramente $\text{Nome}\subseteq \text{(Nome, Cognome)}$)
• allora possiamo dedurre $\text{CF}\to \text{Nome}\in F^A$

dimostrazione

• Se $Z\subseteq Y$, per l’assioma della riflessività, si ha $Y\to Z\in F^A$
• Quindi poiché $X\to Y\in F^A$ e $Y\to Z\in F^A$, per l’assioma della transitività si ha $X\to Z\in F^A$

regola della pseudotransitività

$\text{se }X\to Y\in F^A\text{ e }WY\to Z\in F^A\text{ allora }WX\to Z\in F^A$

esempio

• Se $\text{ID}\to \text{Studente}$
• e $\text{(Corso, Studente)}\to \text{Voto}$
• allora $\text{(Corso, ID)}\to \text{Voto}$

dimostrazione

• Se $X\to Y\in F^A$, per l’assioma dell’aumento si ha $WX\to WY\in F^A$
• Quindi poiché $WX\to WY\in F^A$ e $WY\to Z\in F^A$, per l’assioma della transitività si ha $WX\to Z\in F^A$

osservazione

Osserviamo che:

• per la regola dell’unione, se $X\to A_i\in F^A$, $i=1,\dots ,n$ allora $X\to A_1,\dots ,A_i\dots A_n\in F^A$
• per la regola della decomposizione, se $X\to A_1,\dots ,A_n$ allora $X\to A_i\in F^A\forall i=1,\dots ,n$
• quindi $X\to A_1,\dots ,A_n\in F^A⟺X\to A_i\in F^A\forall i=1,\dots ,n$

ovvero possiamo limitarci in generale a considerare le dipendenze con un dipendente singleton.

chiusura di un insieme di attributi

Sia R uno schema di relazione, F un insieme di dipendenze funzionali su R, e X un sottoinsieme di R. La chiusura di X rispetto a F, denotata con $X_F^{+}$ (o $X^{+}$), è definita come: $X_F^{+}=\{A|X\to A\in F^A\}$

• essenzialmente, fanno parte della chiusura di un insieme di attributi X tutti quelli che sono determinati funzionalmente da X eventualmente applicando gli assiomi di Armstrong.
• banalmente: $X\subseteq X_F^{+}$

esempio

• $\text{CF}\to \text{COMUNE}$
• $\text{COMUNE}\to \text{PROVINCIA}$

$\text{CF}\to \text{COMUNE}$ è diretta, mentre $\text{CF}\to \text{PROVINCIA}$ è indiretta

$${\text{CF}}_F^{+}=\{\text{COMUNE, PROVINCIA, CF}\}$$

determinare la chiave di una relazione

La chiusura di un insieme di attributi ci può essere utile per determinare le chiavi di una relazione.

esempio

• $\text{Auto(MODELLO, MARCA, CILINDRATA, COLORE)}$
• $F=\{\text{MODELLO}\to \text{MARCA, MODELLO }\to \text{COLORE}\}$

Le chiusure sono:

• $(\text{MODELLO}{)}_F^{+}=\{\text{MODELLO, MARCA, COLORE}\}$
• $(\text{MARCA}{)}_F^{+}=\{\text{MARCA}\}$
• $(\text{CILINDRATA}{)}_F^{+}=\{\text{CILINDRATA}\}$
• $(\text{COLORE}{)}_F^{+}=\{\text{COLORE}\}$

Il che ci fa capire che: $\text{chiave}=\text{MODELLO, CILINDRATA}$ (modello e cilindrata, insieme, determinano tutti gli altri)

---

lemma 1

Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$. Si ha: $X\to Y\in F^A⟺Y\subseteq X^{+}$

dimostrazione

Sia $Y=A_1,A_2,\dots ,A_n$

• (dimostro $X\to Y\in F^A⟸Y\subseteq X^{+}$)

Poiché $Y\subseteq X^{+}$, per ogni $i$, $i=1,\dots ,n$ si ha che $X\to A_i\in F^A$. Pertanto per la regola dell’unione, $X\to Y\in F^A$

• (dimostro $X\to Y\in F^A⟹Y\subseteq X^{+}$)

Poiché $X\to Y\in F^A$, per la regola della decomposizione si ha che, per ogni $i$, $i=1,\dots ,n$, $X\to A_i\in F^A$, cioè $A_i\in X^{+}$ per ogni $i,i=1,\dots ,n$, e, quindi, $Y\subseteq X^{+}$

teorema: $F^{+}=F^A$

Siano $R$ uno schema di relazione ed $F$ un insieme di dipendenze funzionali su $R$. Si ha: $F^{+}=F^A$

dimostrazione

$F^A\subseteq F^{+}$

Sia $X\to Y\in F^A$. Dimostriamo che $X\to Y\in F^{+}$ per induzione su $i$ applicazioni di uno degli assiomi di Armstrong.

caso base: ($i=0$): $X\to Y\in F⟹X\to Y\in F^{+},,,,F\subseteq F^{+}$

• (se $X\to Y\in F^A$ senza che abbiamo applicato nessun assioma di Armstrong, allora $X\to Y$ è in $F$ e quindi banalmente è in $F^{+}$)

ipotesi induttiva ($i>0$): $X\to Y\in F^A⟹X\to Y\in F^{+}⟹X\to Y$ è soddisfatto da ogni istanza legale

• (ogni dipendenza in $F^A$ ottenuta applicando fino a $i-1$ assiomi di Armstrong è in $F^{+}$)

passo induttivo: consideriamo $i$: $X\to Y\in F^A$ ottenuto in $i$ passi. Dobbiamo dimostrare che appartiene anch’esso a $F^{+}$

Ci sono tre casi (tre assiomi di Armstrong che potremmo aver applicato all’$i+1$-esimo passo per ottenere $X\to Y$):

1: riflessività

Ho ottenuto $X\to Y$ perché $Y\subseteq X$.

In questo caso, $\forall r\text{ legale},t_1[x]=t_2[x]\wedge Y\subseteq X⟹t_1[y]=t_2[y]$.

(supponiamo che abbiano $X$ uguale: se hanno $X$ uguale e $Y$ è un sottoinsieme di $X$, logicamente anche $Y$ sarà uguale)

2: aumento

Ho ottenuto $X\to Y$ per aumento su $V\to W\in F^A$. Quindi $V\to W\in F^{+}$ è stata ottenuta in massimo $i-1$ passi e appartiene a $F^{+}$ per ipotesi induttiva.

Ci troviamo quindi nel caso in cui $X=VZ$ e $Y=WZ$ per qualche $Z\subseteq R$.

Sia $r$ un’istanza legale e siano $t_1,t_2$ due tuple di $r$ tali che $t_1[X]=t_2[X]$.

• visto che $X=VZ$ e $Y=WZ$, si ha che $t_1[V]=t_2[V]$ e $t_1[Z]=t_2[Z]$

Per ipotesi induttiva ($V\to W\in F^{+}$):

• da $t_1[V]=t_2[V]$ segue $t_1[W]=t_2[W]$
• da $t_1[W]=t_2[W]\wedge t_1[Z]=t_2[Z]$ segue $t_1[Y]=t_2[Y]$ (perché $Y=WZ$)

3: transitività

Ho ottenuto $X\to Y$ per transitività da $X\to Z$ e $Z\to Y$ in $F^A$.

• le due dipendenze sono state ottenute in massimo $i-1$ e appartengono a $F^{+}$ per ipotesi induttiva

Sia $r$ un’istanza legale di $R$ e siano $t_1,t_2$ tali che $t_1[X]=t_2[X]$. Per ipotesi induttiva, da $t_1[X]=t_2[X]$ segue $t_1[Z]=t_2[Z]$, da cui, sempre per ipotesi induttiva, segue $t_1[Y]=t_2[Y]$.

$F^{+}\subseteq F^A$

Supponiamo per assurdo che esita una dipendenza funzionale $X\to Y\in F^{+}$ tale che $X\to Y\notin F^A$.

Consideriamo la seguente istanza $r$ di $R$:

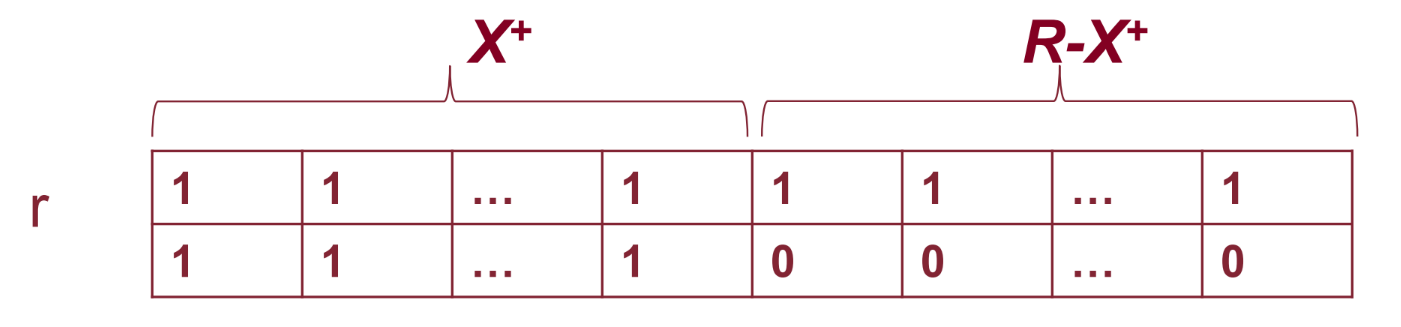
Ha due tuple uguali su tutti gli attributi di $X^{+}$ e diverse su tutti gli altri.

mostriamo che $r$ è un’istanza legale

Sia $V\to W$ una dipendenza funzionale in $F$.

• se le tuple sono diverse su $V$ (e quindi $V\cap R-X^{+}\ne \varnothing$), allora la dipendenza è soddisfatta ($t_1[V]\ne t_2[V]$)

Se invece due tuple di $r$ hanno gli stessi valori per $V$, allora sappiamo necessariamente che $V\subseteq X^{+}$ e quindi (Lemma 1) $X\to V\in F^A$.

• sappiamo che $V\to W\in F$, quindi $V\to W\in F^A$, quindi
  • per l’assioma della transitività ($X\to V,V\to W$) otteniamo che $X\to W\in F^A$
• quindi, di nuovo per il Lemma 1, $W\subseteq X^{+}$, ovvero le due tuple sono uguali anche su $W$.
  • quindi $V\to W$ è soddisfatta.

visto che $r$ soddisfa $V\to W$ in entrambi i casi, e $V\to W$ è una dipendenza qualsiasi di $F$, allora le rispetta tutte (ed è quindi un’istanza legale).

usiamo $r$ per dimostrare l’inclusione

Visto che $r$ è un’istanza legale, essa deve soddisfare ogni $X\to Y\in F^{+}$. Dobbiamo mostrare $X\to Y\in F^{+}⟹X\to Y\in F^A$.

Sappiamo che $X\subseteq X^{+}$, e quindi sappiamo che le tuple di $r$ corrispondono su $X$. Poiché $r$ soddisfa $X\to Y$, quindi, devono anche corrispondere su $Y$. Abbiamo quindi $Y\subseteq X^{+}$, e, per il Lemma 1, $X\to Y\in F^A$.

Abbiamo quindi mostrato che $X\to Y\in F^{+}⟹X\to Y\in F^A$.

domande orale

possibili domande

• elencare gli assiomi di Armstrong
• elencare (e dimostrare) gli assiomi “conseguenze”
• cos’è la chiusura di un attributo rispetto a un insieme di dipendenze?
• cos’è $F^{+}$? si può calcolare?
• cosa c’è dentro $F^{+}$ se $F$ è vuoto? (le dipendenze banali)
• lemma 1 (e dimostrazione)
• dimostrare $F^{+}=F^A$