6 - individuare cicli

Dato un grafo $G$ (diretto o indiretto), vogliamo sapere se esso è ciclico

Un’idea (errata) di partenza potrebbe essere quella di visitare un grafo e, se si incontra un nodo già visitato, interrompere la visita e restituire $\text{True}$ (e, altrimenti, restituire $\text{False}$), ma:

• non funziona con i grafi indiretti perché in un grafo indiretto, se $(u,v)\in E$, anche $(v,u)\in E$, quindi nella lista di adiacenza di $u$ ci sarà $v$ e viceversa ⇒ ogni arco verrebbe considerato un ciclo e farebbe ritornare True
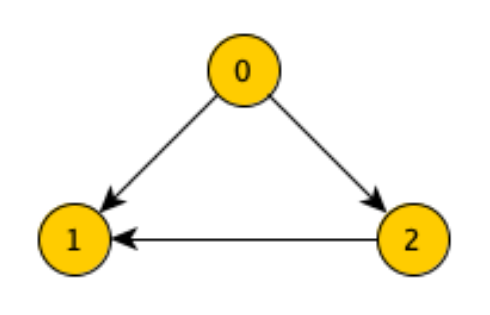
• non funziona neanche con alcuni grafi diretti: prendiamo come esempio il grafo $[[1,2],[],[1]]$: partendo dal nodo $0$, si visita prima il nodo $1$ (che non ha archi uscenti), e poi il nodo $2$. Ma il nodo $2$ ha un arco uscente verso $1$ (già visitato) ⇒ l’algoritmo ritornerebbe quindi $\text{True}$, nonostante non ci siano cicli.
• 

algoritmo per grafi indiretti

Per il caso dei grafi indiretti, si può risolvere il problema tenendo traccia del nodo padre ed escludendolo dai controlli.

def DFSc(u, padre, G, visitati):
	visitati[u] = 1
	for v in G[u]:
		if visitati[v] == 1:
			if v != padre:
				return True
		else:
			if DFSc(v, u, G, visitati):
				return True
	return False
 
def ciclo(u, G):
	visitati = [0]*len(G)
	return DFSc(u, u, G, visitati)

Questo algoritmo ha complessità $O(n)$ perché:

• se il grafo non contiene cicli, avrà al più $n-1$ archi e $O(n+m)=O(n)$
• se contiene cicli, se ne scopre uno dopo aver considerato al più $n$ archi

algoritmo per grafi diretti

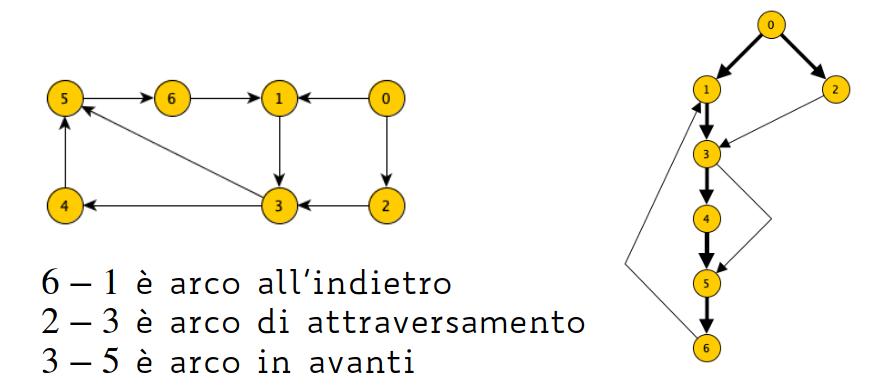
Si nota che durante la visita DFS, si possono incontrare nodi già visitati in 3 casi:

1. archi in avanti (da un antenato a un discendente)
2. archi all’indietro (da un discendente a un antenato)
3. archi di attraversamento (tutti gli altri)

Solo gli archi all’indietro mostrano la presenza di un ciclo (un nodo punta a un suo antenato).

diversi tipi di archi

Serve quindi un modo di distinguere i tre casi. Si nota che solo nel caso degli archi all’indietro la visita di un nodo non ha terminato la sua sezione ricorsiva.

Basta quindi modificare il vettore dei visitati in modo che i suoi valori siano:

• $0$ se il nodo non è ancora stato visitato
• $1$ se il nodo è stato visitato, ma la ricorsione su di esso non è ancora finita
• $2$ se il nodo è stato visitato e la ricorsione su di esso è finita

In questo modo, scopro un ciclo quando trovo un arco diretto verso un nodo già visitato che si trova nello stato $1$.

algoritmo corretto:

def DFSc(u, G, visitati):
	visitati[u] = 1
	for v in G[u]:
		if visitati[v] == 1: return True # stato "in elaborazione"
			
		if visitati[v] == 0:
			if DFSc(v, G, visitati): return True
	
	visitati[u] = 2 # nodo completamente esplorato
 
# se so già da che nodo partire:
def cicloD(u, G)
	visitati = [0]*len(G)
	return DFSc(u, G, visitati)
 
# se non so da che nodo partire:
def cicloD(G):
	visitati = [0]*len(G)
	for u in range(len(G)):
		if visitati[u] == 0:
			if DFSc(u, G, visitati):
				return True
	return False

• la complessità è $O(n+m)$ in entrambi i casi