2 - visita DFS

concetti base

raggiungibilità

Un nodo $u$ è raggiungibile da un nodo $v$ se esiste almeno un cammino che da $u$ arriva a $v$.

connettività

Il problema della connettività si occupa di determinare se, comunque prendo due nodi $u$ e $v$, tra essi c’è un cammino.

Depth-First Search (DFS)

La strategia della visita depth-first consiste nel visitare il grafo sempre più “in profondità” (unexpected), quando possibile. Partendo da un nodo, si prosegue lungo un sentiero finché non si arriva a un nodo che non ha più archi da seguire, quindi si torna indietro per esplorare eventuali altri archi dai nodi già visitati. Durante tutta la ricerca, non si visitano mai (all‘“andata”) nodi già visitati, per non cadere in cicli.

visita DFS su grafo rappresentato tramite matrice di adiacenza:

• usiamo un vettore dei visitati per tenere conto dei nodi già visitati: quando si trova un nodo $u$, lo si visita solo se $\text{visitati[u]==0}$

def DFS(u, M)
	visitati[u] = 1 
	for i in range(len(M)): # si scorrono i vicini di u - θ(n)
		if M[u][i] and not visitati[i]:
			DFS(i, M, visitati) # O(n) (entro massimo n volte)
			
# ^ quindi questa funzione ha costo O(n)xΘ(n)
 
n = len(M)
visitati = [0]*n # Θ(n)
DFS(u, M, visitati)
return [x for x in range(n) if visitati[x]] # Θ(n)
 
# ^ prendo dai nodi (range della lunghezza delle liste) solo quelli che sono stati visitati

• al termine dell’esecuzione della funzione ricorsiva, si ha $\text{visitati[i]=1}$ se e solo se $i$ è raggiungibile da $u$.
• questo algoritmo ha costo $O(n)\times \Theta (n)=O(n^2)$

visita DFS su grafo rappresentato tramite liste di adiacenza:

def DFS(u, G, visitati):
	visitati[u] = 1
	for v in G[u]:
		if not visitati[v]:
			DFS(v, G, visitati)
 
# ^ questa funzione ha costo O(n+m)
 
n = len(G)
visitati = [0]*n
DFS(u, G, visitati)
return [x for x in range(n) if visitati(x)] # Θ(n)

Per ogni nodo $u$, l’algoritmo scorrerà la lista dei suoi adiacenti. Il ciclo for avrà quindi complessità $|\text{adj }0|+|\text{adj }1+\cdots +|\text{adj }n-1|$ (somma degli elementi nelle liste di tutti i nodi visitati), che, visto che non si visiterà mai un nodo due volte, corrisponde a $m$ (numero di archi) nel caso in cui il grafo è diretto, o $2m$ nel caso di un grafo indiretto.

• in entrambi i casi, la somma di tutte le iterazioni del ciclo for sarà quindi in $O(n)$

Il costo totale sarà quindi $O(n+m)$.

• se il grafo è sparso, $m\in O(n)$, quindi la complessità temporale totale sarà $O(n)$

versione iterativa

def DFS_i(u, G):
	visitati = [0]*len(G)
	stack = [u]
	while stack:
		u = stack.pop()
		if not visitati[u]:
			visitati[u] = 1
			
			for v in G[u]:
				if not visitati[v]:
					stack.append(v)
					
	return [x for x in range(len(G)) if visitati[x]]

• anche qui, la complessità temporale è $O(n+m)$

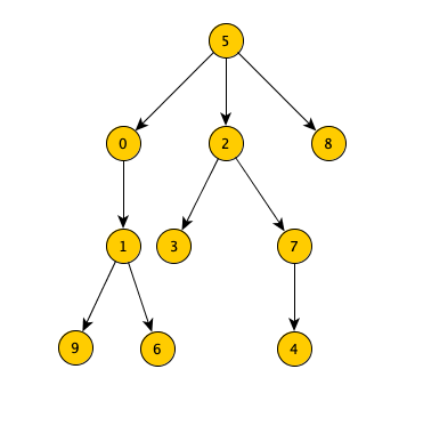
albero DFS

Visto che la ricerca visita solo nodi non precedentemente visitati, con una visita DFS, gli archi del grafo si dividono in attraversati e non attraversati. I nodi visitati e gli archi attraversati formano un albero detto albero DFS.

vettore dei padri

L’albero DFS si può memorizzare tramite il vettore dei padri ⇒ un vettore che contiene, per ogni entrata $i$, l’indice del suo nodo padre.

• (per convenzione, il padre della radice è essa stessa - $P[r]==r$)
• se $i$ non è un nodo dell’albero (in questo caso, se non è stato visitato), $P[i]==-1$

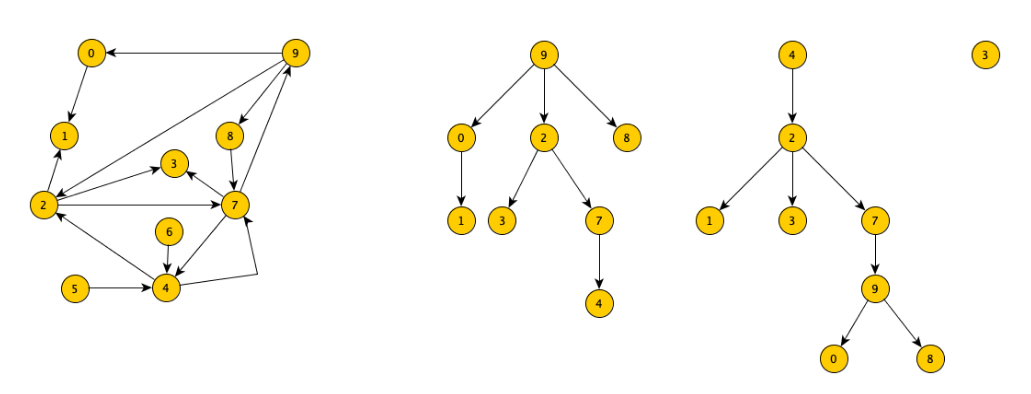
(a sinistra un grafo, a destra i tre alberi DFS che si ottengono partendo dai nodi 9, 4 e 3 rispettivamente)

esempio

per esempio, questo albero sarà rappresentato dal seguente vettore dei padri:

$P=\begin{array}{cccccccccc}5& 0& 5& 2& 7& 5& 1& 2& 5& 1\end{array}$

La visita DFS può essere modificata in modo da memorizzare il vettore dei padri anziché quello dei visitati.

def DFSp(x, G, P):
	for y in G[x]:
		if P[y] == -1:
			P[y] = x
			DFSp(y, G, P)
 
def padri(u, G):
	n = len(G)
	P = [-1]*n
	P[u] = u
	DFSr(u, G, P)
	return P

• al termine dell’algoritmo, $P[v]==-1$ se non è stato visitato. altrimenti, contiene il padre di $v$

trovare un cammino

Molto spesso non basta sapere se un nodo $v$ sia raggiungibile da un nodo $u$, ma si vuole anche determinare un cammino che permetta di arrivare da $u$ a $v$.

• il vettore dei padri rende questa operazione molto semplice: basta controllare che il nodo $v$ sia nell’albero DFS, ed effettuare un reverse dei nodi incontrati

versione iterativa:

def Cammino(u, P):
	if P[u] ==  -1: return [] # se non è nell'albero (non visitato)
	path = []
	while P[u] != u: # se P[u] = u, siamo arrivati al nodo che cerchiamo
		path.append(u)
		u = P[u] # seguiamo i padri
	path.append(u)
	path.reverse()
	return path

versione ricorsiva:

def CamminoR(u, P):
	if P[u] == -1: return []
	if P[u] == u: return [u]
	return CamminoR(P[u], P) + [u]

• in entrambi i casi, disponendo del vettore dei padri, la complessità è $O(n)$

attenzione

se esistono più cammini da $u$ a $v$, la procedura non garantisce la restituzione del cammino minimo