5 - ordinamento topologico

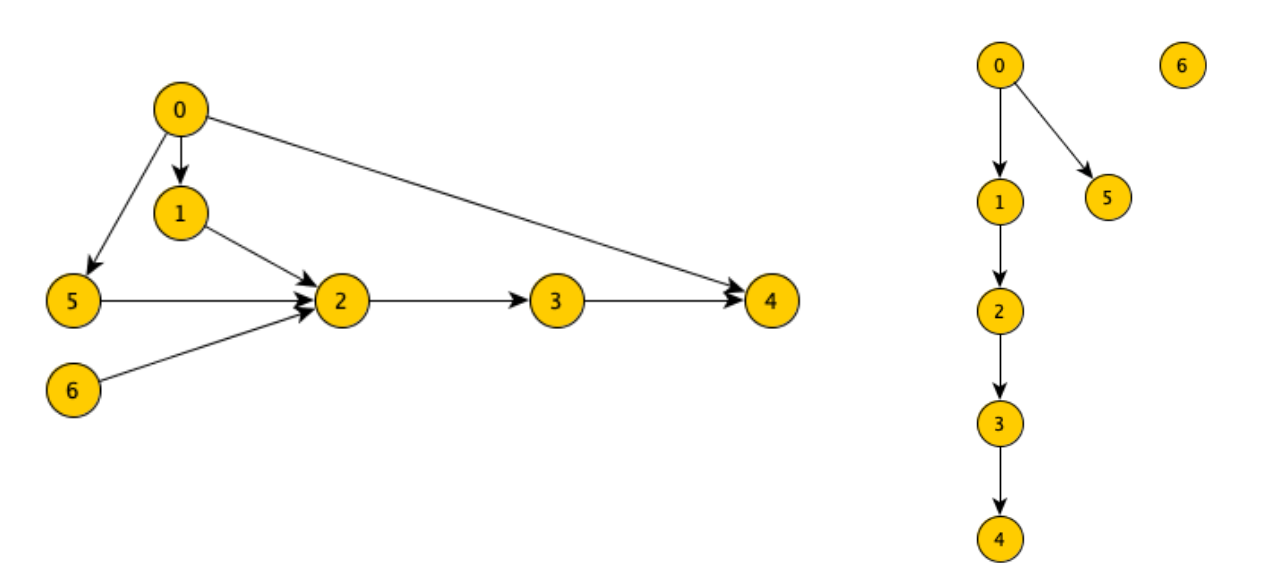
Un ordinamento topologico è una permutazione dei nodi di un grafo tale che, se $(u,v)\in E$, allora $u$ compare prima di $v$ nell’ordinamento (ovvero tutte le frecce puntano in una sola direzione).

• non è sempre possibile trovarne uno

Un grafo diretto può avere da $0$ a $n!$ ordinamenti topologici (ha il massimo numero di ordinamenti topologici quando non ha archi - tendenzialmente, più archi ci sono, meno sono gli ordinamenti topologici)

esiste un sort topologico $⟺$ il grafo è un DAG (grafo diretto aciclico)

Un DAG ha infatti sempre un nodo sorgente, ovvero un nodo in cui non entrano archi. Questa proprietà ci permette di costruire un ordinamento topologico in questo modo:

• inizio la sequenza dei nodi con una sorgente
• cancello dal DAG quel nodo sorgente e gli archi che partono da esso - otterrò un nuovo DAG
• ripeto fino ad aver sistemato in ordine lineare tutti i nodi

fatto anche qui (basi di dati 1, serializzabilità)

algoritmo per il sort topologico (basato sulle sorgenti)

• restituisce un sort topologico di $G$ se esiste - altrimenti, una lista vuota

def sortTop(G):
	n = len(G)
	gradoEnt = [0]*n
	for i in range(n):
		for j in G[i]:
			gradoEnt[j] += 1 
			# se j compare in una qualsiasi lista di adiacenza, 
			# vuol dire che ha archi entranti
 
	sorgenti = [ i for i in range(len(G)) if gradoEnt[i]==0 ]
	ST = []
 
	while sorgenti:
		u = sorgenti.pop()
		ST.append(u)
		for v in G[u]:
			gradoEnt[v] -= 1
			if gradoEnt[v] == 0:
				sorgenti.append(v)
 
	if len(ST) == len(G): return ST
	return []

• creare il vettore dei gradi entranti costa $O(n+m)$
• inizializzare l’insieme delle sorgenti costa $O(n)$
• il while viene eseguito $O(n)$ volte e il costo totale del for al termine del while è $O(m)$

il costo totale è quindi $O(n+m)$.

algoritmo per il sort topologico basato su DFS

• si effettua una visita DFS
• man mano che termina la visita dei vari nodi, si inseriscono in una lista
• si restituisce come ordinamento dei nodi il reverse della lista

prova di correttezza

Siano $x$ e $y$ due nodi in $G$, con arco $(x,y)$. Consideriamo sia il caso in cui l’arco viene attraversato che quello in cui non viene attraversato dalla visita, e vediamo che in entrambi, prima di effettuare il reverse, $x$ precede $y$.

1. l’arco $(x,y)$ viene attraversato durante la visita ⇒ la visita di $y$ finisce prima della visita di $x$, e $y$ finisce nella lista prima di $x$
2. l’arco $(x,y)$ non viene attraversato durante la visita ⇒ significa che il nodo $y$ è già stato visitato prima della visita di $x$, e la sua visita è già terminata (infatti, non può esserci un cammino $y\to x$, o il grafo non sarebbe aciclico). Quindi, anche in questo caso, $y$ si trova prima di $x$ nella lista.

esempio

$\text{ordine di fine visita: }4,3,2,1,5,0,6$ (il sort topologico sarà quindi $6,0,5,1,2,3,4$)

def DFS(u, G, visitati, lista):
	visitati[u] = 1
	for v in G[u]:
		if visitati[v] == 0:
			DFSr(v, G, visitati, lista)
	lista.append(u)
 
def sortTop1(G):
	visitati = [0]*len(G)
	lista = []
	for u in range(len(G)):
		if visitati[u] == 0:
			DFS(u, G, visitati, lista)
	lista.reverse()
	return lista

La complessità di questo algoritmo è $O(n+m)$ (perché nella DFS si visitano sempre nodi diversi) $+O(n)$ (per il reverse()), ovvero $O(n+m)$.

perche non appendere in testa ?

Il costo di un append in testa è proporzionale alla dimensione della lista, quindi, per la sommatoria di Gauss, il loro costo totale arriverebbe a $\Theta \left(\frac{n(n-1)}{2}\right)=\Theta (n^2)$. Appendere in coda invece costa sempre $O(1)$, e il reverse costa $O(n)$.