10 - minimo albero di copertura

spanning tree

Dato un grafo $G$, un albero di copertura (o ricoprente/di connessione/di supporto) è un qualsiasi sottografo $G^{\prime }=(V^{\prime },E^{\prime })$ con $V^{\prime }=V$, $E^{\prime }\subseteq E$ che sia un albero (quindi che sia connesso e aciclico).

• (un albero di copertura di un grafo connesso indiretto è un albero che contiene tutti i nodi del grafo e contiene soltanto un sottoinsieme degli archi: quelli necessari per connettere tra loro tutti i vertici con uno e un solo cammino)

minimum spanning tree

Sia $G$ un grafo indiretto connesso pesato. Un albero di copertura minimale è un suo albero di copertura $T\subseteq G$ tale che la somma di tutti i pesi degli archi di $T$ è minima rispetto a quella di tutti gli altri alberi di copertura.

• un MST non è unico

se si ha un sottografo $G^{\prime }=(V^{\prime },E^{\prime })$ connesso tale che $V^{\prime }=V$ e tale che la somma dei pesi dei suoi archi sia minima, allora $G^{\prime }$ è necessariamente un albero (e quindi un MST)

• (sappiamo che albero = grafo connesso indiretto aciclico)
• supponiamo che ci sia un ciclo in $G^{\prime }$: vorrebbe dire che esiste almeno un arco che può essere eliminato senza che il grafo perda la sua connessione: questo contraddirebbe l’ipotesi per cui la somma dei pesi degli archi di $G^{\prime }$ è minima. È perciò impossibile che ci siano cicli, e $G^{\prime }$ (poiché $V^{\prime }=V$ e $G^{\prime }$ connesso) è quindi un albero.

Il problema è quindi trovare un sottoinsieme di archi che colleghi tutti i vertici e che abbia il minimo peso totale.

algoritmo di Kruskal

L’algoritmo di Kruskal fornisce una soluzione al problema del minimo albero di copertura.

La logica che segue è questa:

• parte con il grafo $T$ che contiene tutti i nodi di $G$ e nessun arco di $G$
• considera uno alla volta gli archi del grafo $G$ in ordine di costo crescente
• se un arco non forma un ciclo in $T$ con archi già considerati, lo inserisce in $T$
• al termine restituisce $T$

Anche questo algoritmo rientra nel paradigma della programmazione greedy:

• (decisioni irrevocabili) una volta deciso se inserire o meno un arco in $T$, non ritorna più sulla decisione
• (decisioni prese in base ad un criterio locale) se un arco crea un ciclo, non lo si aggiunge; altrimenti, lo si sceglie in quanto è il meno costoso a non creare cicli

pseudocodice:

kruskal(G):
	T = set()
	inizializza E con gli archi di G
	while E != []:
		estrai da E un arco (x,y) di peso minimo
		if l'inserimento di (x,y) non crea ciclo con gli archi in T:
			inserisci arco (x,y) in T
	return T

dimostrazione di correttezza

correttezza

Dobbiamo mostrare che, al termine dell’algoritmo, $T$ è un albero di copertura e che non c’è un altro albero che costa meno.

1. produce un albero di copertura

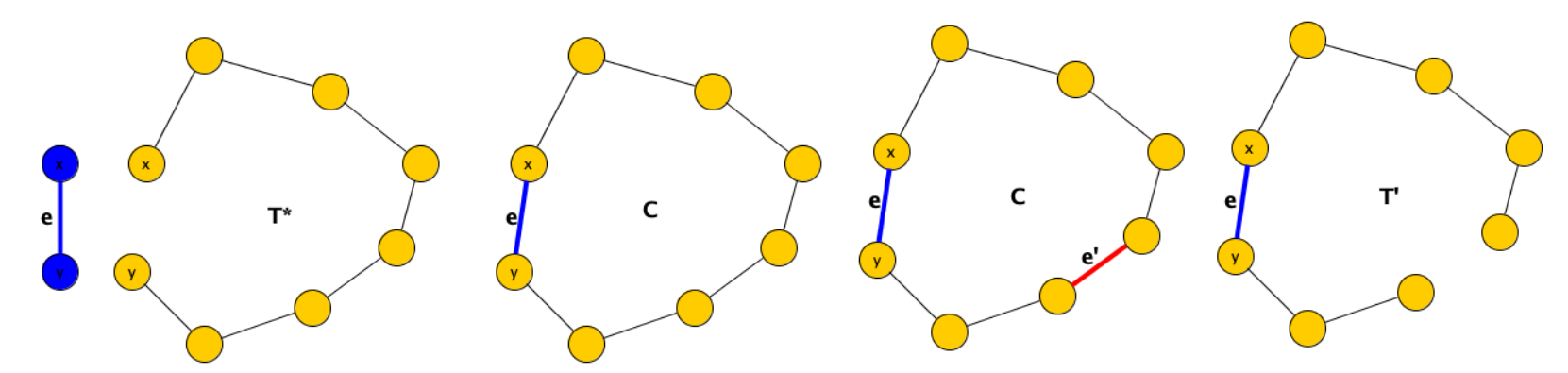
Supponiamo, per assurdo, che al termine dell’algoritmo il sottoinsieme $T$ di archi non sia connesso. In tal caso, $T$ avrebbe più di una componente connessa. Poiché il grafo iniziale $G$ è connesso, esiste almeno un arco $(x,y)$ che connette due nodi $x$ e $y$ di due componenti diverse di $T$.

Se $(x,y)$ non è stato inserito in $T$, significa che è stato scartato perché avrebbe creato un ciclo. Tuttavia, dato che $(x,y)$ connette due componenti disconnesse, non potrebbe formare un ciclo, poiché non esiste un percorso precedente in $T$ che collega $x$ a $y$. Questo porta a una contraddizione, in quanto l’algoritmo scarta solo gli archi che causano cicli. Pertanto, il grafo $T$ deve essere connesso e aciclico (ovvero un albero).

2. non c’è un albero di copertura per $G$ che costa meno dell’albero $T$ ottenuto

Sia $T$ l’albero di copertura prodotto dall’algoritmo di Kruskal, e sia $T^{\ast }$ un altro albero di copertura con lo stesso costo minimo. Assumiamo che $T$ e $T^{\ast }$ differiscano: supponiamo che $T^{\ast }$ sia l’albero di copertura con lo stesso costo che differisce nel minor numero di archi da $T$. (il numero di archi dei due rimane lo stesso, ma hanno x archi diversi con x minimo)

Consideriamo l’ordine $e_1,e_2,\dots$ con cui gli archi sono stati presi in considerazione nel corso dell’algoritmo. Sia $e$ il primo arco che compare in $T$ e non in $T^{\ast }$. Se $e$ fosse inserito in $T^{\ast }$, creerebbe un ciclo $C$ (perché $T^{\ast }$ è un albero di copertura, quindi l’aggiunta di un altro arco genererebbe necessariamente un ciclo). Il ciclo $C$ contiene almeno un arco $e^{\prime }$ che non appartiene a $T$ (se tutti gli archi di $C$ fossero in $T$, allora l’algoritmo non avrebbe aggiunto $e$).

Consideriamo ora l’albero $T^{\prime }$, ottenuto da $T^{\ast }$ inserendo $e$ ed eliminando $e^{\prime }$. Il costo del nuovo albero $T^{\prime }$ è $costo(T^{\ast })-costo(e^{\prime })+costo(e)$. Questo non può aumentare rispetto a quello di $T^{\ast }$, perché $costo(e)\le costo(e^{\prime })$ (perché tra $e$ ed $e^{\prime }$, Kruskal ha considerato prima $e$).

Quindi, $T^{\prime }$ è un altro albero di copertura ottimo che differisce da $T$ in meno archi di quanto faccia $T^{\ast }$ (perché, rispetto a $T^{\ast }$, al posto dell’arco $e^{\prime }$ ha l’arco $e$, che appartiene a $T$), il che contraddice l’ipotesi per cui $T^{\ast }$ differisce da $T$ nel minor numero di archi.

implementazione

• con un pre-processing, ordino gli archi nella lista $E$ così che, scorrendola, ottengo di volta in volta l’arco di costo minimo in tempo $O(1)$
• verifico che l’arco $(x,y)$ non formi ciclo in $T$ controllando se $y$ è raggiungibile da $x$ in $T$

def kruskal(G):
	E = [(c,u,v) for un in range(len(G)) for v,c in G[u] if u < v]
	E.sort()
	T = [[] for _ in G]
	
	for c,u,v in E:
		if not connessi(u,v,T):
			T[u].append(v)
			T[v].append(u)
	return T

def DFSr(a, b, T, visitati):
	visitati[a] = 1
	for z in T[a]:
		if z == b:
			return True
		if not visitati[z]:
			if DFSr(z, b, T, visitati):
				return True
	return false
 
def connessi(u,v,T):
	visitati = [0]*len(T)
	return DFSr(u, v, T, visitati)

• l’ordinamento esterno al for costa $O(m\log m)=O(m\log n)$
  • ($m\log m\le m\log n^2=2m\log n\in O(m\log n)$)
• il for fa $m$ iterazioni, e controllare che l’arco $(a,b)$ non crei un ciclo in $T$ costa quanto la visita di un grafo aciclico, ovvero $O(n)$
  • il for richiede quindi $O(m\cdot n)$

La complessità totale è $O(m\cdot n)$.

implementazione con union-find in $O(m\log n)$

Union-Find (o Disjoint Set Union) è una struttura dati per gestire insiemi disgiunti che permette operazioni di unione e ricerca efficienti.

In questo caso, gli insiemi disgiunti rappresentano le componenti connesse del grago.

operazioni fondamentali

Le tre operazioni fondamentali di Union-Find sono:

• Crea(C): restituisce una struttura dati Union-Find sull’insieme S di elementi dove ciascun elemento è in un insieme separato
• Find(x,C): restituisce il nome dell’insieme nella struttura dati C a cui appartiene l’elemento x
• Union(A,B,C): modifica la struttura dati C fondendo la componente A con la componente B e restituisce il nome della nuova componente

L’operazione Find() ci permette di determinare a quale componente connessa appartenga un nodo $u$, e può essere sfruttata per determinare se due nodi $u$ e $v$ appartengono alla stessa componente.

• se viene aggiunto l’arco $(u,v)$ al grafo si verifica quindi innanzitutto se $u$ e $v$ sono nella stessa componente connessa e, se non lo sono, si utilizza l’operazione Union() per unire le due componenti.

Un modo efficiente di implementare questa struttura dati è mediante vettore dei padri. In questo modo, l’operazione Find() ha costo $O(n)$, in quanto basta risalire alla radice del nodo, e l’operazione Union() costa $O(1)$, in quanto basta rendere una delle due componenti figlia dell’altra.

Ma il costo della Find() si può ridurre ancora per arrivare a un costo di $O(\log n)$ se, ogni volta che si effettua una Union(), si sceglie come nuova radice l’albero che contiene il maggior numero di elementi.

dimostrazione

Dimostriamo che, facendo unioni in base all’altezza (union by rank), si mantiene la proprietà per cui, se una componente ha altezza $h$, essa conterrà almeno $2^h$ nodi, dalla quale possiamo dedurre che l’altezza delle componenti (e quindi il costo della Find()) non supererà mai ${\log }_{2}n$.

• ($2^{{\log }_{2}n}=n$, quindi, se $h>\log n$, si avrebbero più di $n$ elementi in una componente, il che è impossibile)

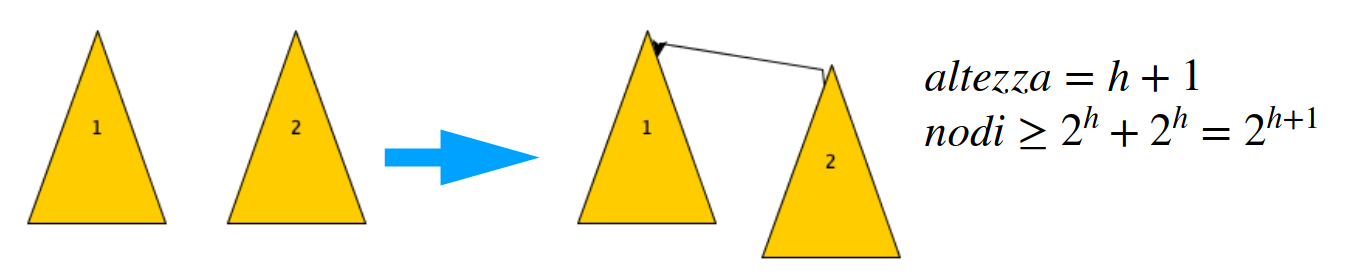
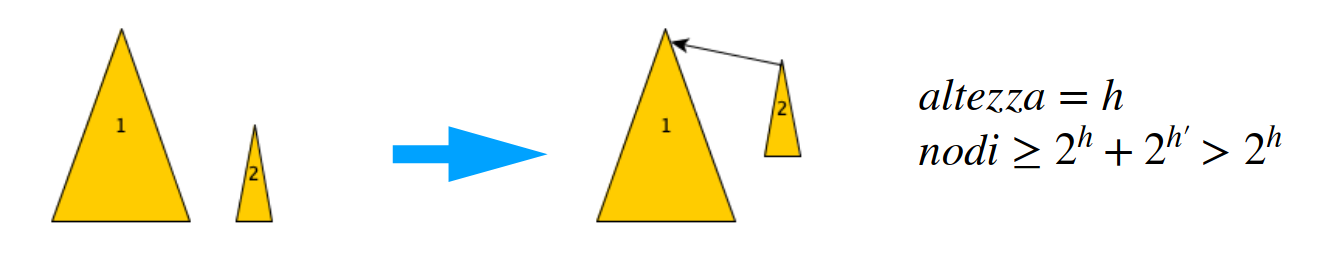
Assumiamo per assurdo che durante una delle fusioni si sia formata una nuova componente di altezza $h$ per cui la proprietà non è valida. Siano $ca$ e $cb$ le due componenti la cui fusione ha generato la nuova componente.

Possono essere accadute due cose:

1. $ca$ e $cb$ erano componenti con la stessa altezza

$ca$ e $cb$ avevano entrambe altezza $h-1$ e ognuna aveva almeno $2^{h-1}$ elementi (perché nelle fusioni precedenti la proprietà era valida). Il numero totale di elementi della nuova componente è $2^{h-1}+2^{h-1}=2^h$ ⇒ la proprietà è verificata.

2. altezza di $ca$ > altezza $cb$

In questo caso, l’altezza dopo la fusione sarà necessariamente quella di $ca$. (Infatti, l’altezza di $cb$ aumenterà di 1 (la nuova radice), e la situazione sarà $ca\ge cb$). $ca$ conteneva già da sola $2^h$ elementi, quindi la proprietà è verificata.

L’implementazione delle operazioni deve quindi tenere conto del numero di elementi in ogni componente. Ogni elemento sarà caratterizzato da una coppia $(x,numero)$ dove $x$ è il nome dell’elemento e $numero$ è il numero di nodi dell’albero radicato in $x$.

def Crea(G):
	C = [(i,1) for i in range(len(G))] # si inizializza con una componente per nodo
	return C

def Find(u, C):
	while u != C[u]:
		u = C[u]
	return u

def Union(a, b, C):
	tota, totb = C[a][1], C[b][1]
	if tota >= totb:
		C[a] = (a, tota + totb) # a nuova radice
		C[b] = (a, totb)
	else:
		C[a] = (b, tota)
		C[b] = (b, tota + totb) # b nuova radice

l’implementazione di Kruskal sarà quindi:

def kruskal(G):
	E = [(c, u ,v) for u in G for v,c in G[u] if u < v]
	E.sort()
	T = [[] for _ in G]
	C = crea(T)
	for c, u ,v in E:
		cu = find(u, C)
		cv = find(v, C)
		if cu != cv:
			T[x].append(y)
			T[y].append(x) 
	return T

• l’ordinamento costa $O(m\log n)$
• il for viene iterato $m$ volte
  • l’estrazione dell’arco $(a,b)$ da $E$ costa $\Theta (1)$
  • il Find() costa $O(\log n)$
  • la Union() costa $\Theta (1)$ e viene eseguita $n-1$ volte all’interno del for
  • for costa quindi $O(m\log n)$

Il costo totale è $O(m\log n)$.