7 - ponti

ponte

Un ponte è un arco la cui eliminazione disconnette un grafo (ovvero aumenta il numero di componenti connesse). Equivalentemente, un arco è un ponte se e solo se non è contenuto in nessun ciclo.

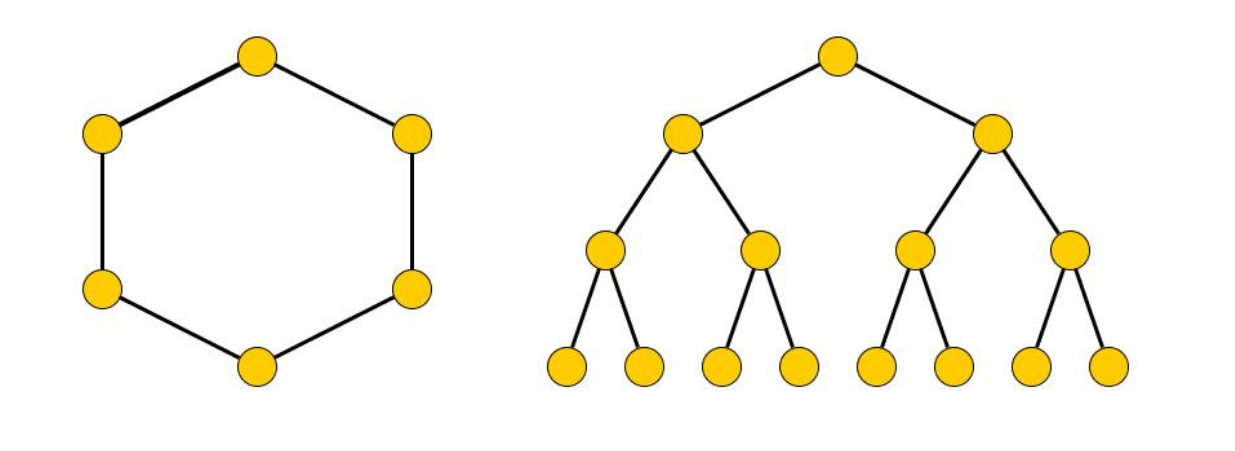
• un grafo può non avere nessun ponte (esempio: un ciclo), o essere composto esclusivamente da ponti (esempio: un albero)

determinare l’insieme dei ponti di un grafo

Una prima soluzione si basa sulla ricerca esaustiva: si prova, per ogni arco del grafo, se questo è un ponte o no.

Verificare se un arco $(a,b)$ è un ponte per $G$ richiede $O(m)$: basta eliminare l’arco $(a,b)$ da $G$ ed effettuare una DFS per controllare se $b$ rimane raggiungibile da $a$.

• la complessità sarebbe $m\cdot O(m)=O(m^2)=O(n^4)$

Il problema è in realtà risolvibile in $O(m)$, usando un'unica visita DFS

L’intuizione si basa sul fatto che i ponti vanno ricercati unicamente tra i $n-1$ archi dell’albero DFS:

• un arco non presente nell’albero DFS non può essere ponte perché, anche se venisse eliminato, gli archi dell’albero DFS garantirebbero la connessione.

Notiamo che gli archi che non sono ponti sono coperti da archi non attraversati durante la visita.

proprietà

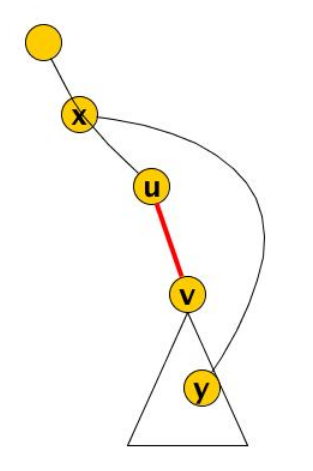
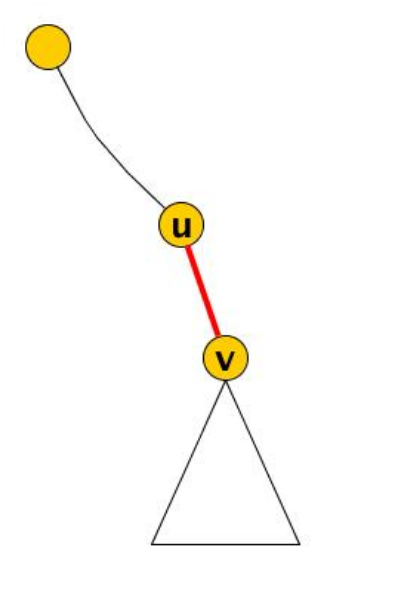
Sia $(u,v)$ un arco dell’albero DFS con $u$ padre di $v$. L’arco $u-v$ è un ponte se e solo se non ci sono archi tra i nodi del sottoalbero radicato in $v$ e il nodo $u$ o nodi antenati di $u$

dimostrazione

• $⟹$

Supponiamo per assurdo che $x-y$ sia un arco tra un antenato di $u$ e un disccendente di $v$. Dopo l’eliminazione di $u-v$, tutti i nodi dell’albero resterebbero connessi grazie all’arco $x-y$

• $⟸$

In questo caso, l’eliminazione dell’arco $u-v$ disconnette i nodi dell’albero radicato in $v$ dal resto del grafo. Infatti, tutti gli archi che non appartengono all’albero e che partono da nodi nel sottoalbero di $v$ vanno verso $v$ o un suo discendente.

La logica da seguire è quindi questa:

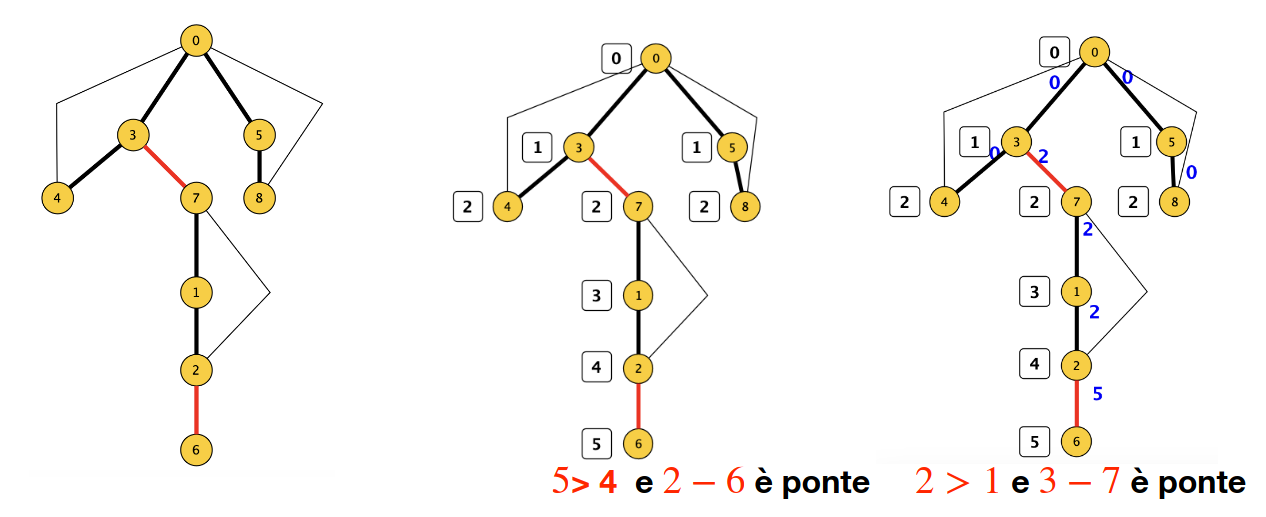
Per ogni arco padre-figlio $(u,v)$ presente nell’albero DFS, il nodo $u$ è in grado di scoprire se l’arco $(u,v)$ è un ponte in questo modo: per ogni nodo $v$:

• calcola la sua altezza nell’albero
• calcola e restituisce al padre $u$ l’altezza minima che si può raggiungere con archi che partono da nodi del suo sottoalbero diversi da $(u,v)$

Il nodo $u$ confronta la sua altezza con quella ricevuta: perché sia ponte, l’altezza di $u$ deve essere minore di quella restituita dal figlio.

quindi

• nodo $v$ ⇒ esplora il proprio sottoalbero e restituisce $b$: il minimo livello da sé raggiungibile (utilizzando anche archi all’indietro)
• nodo $u$ ⇒ confronta $b$ con la propria altezza - se $b>\text{altezza}$, l’arco $(u,v)$ è un ponte (è l’unico collegamento); altrimenti, un c’è un percorso alternativo e l’arco non è un ponte

def DFSp(G, x, padre, altezza, ponti):
	if padre == -1:
		altezza[x] = 0 # primo nodo
	else:
		altezza[x] = altezza[padre] + 1
	
	min_raggiungibile = altezza[x]
	
	for y in G[x]:
		if altezza[y] == -1: # non visitato
			b = DFSp(y, x, altezza, ponti)
			
			if b > altezza[x]:
				ponti.append((x,y))
			
			min_raggiungibile = min(min_raggiungibile, b)
		
		elif y != padre: # già visitato ma non padre: arco all'indietro
			min_raggiungibile = min(min_raggiungibile, altezza[y])
			
			# visto che (x,y) è un arco all'indietro, il min raggiungibile sarà sicuramente <= altezza[y] (y potrebbe arrivare ancora più indietro)
	
	return min_raggiungibile
 
def ponti(G):
	altezza = [-1]*len(G)
	ponti = []
 
	DFSp(G, 0, -1, altezza, ponti) 
	# i ponti si troveranno dentro "ponti"