4 - componenti connesse

Una componente connessa (o semplicemente “componente”) di un grafo indiretto è un sottografo composto da un insieme massimale di nodi connessi da cammini.

grafo connesso

Un grafo indiretto si dice connesso se ha una sola componente.

esempio di grafo con 5 componenti:

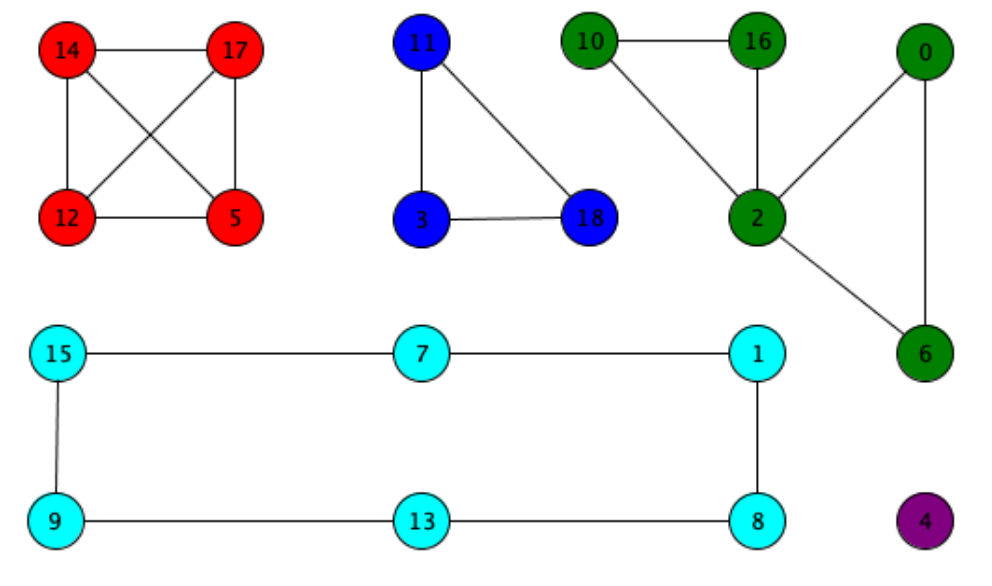
Si può calcolare il vettore delle componenti connesse di un grafo $G$. Il vettore ($C$) ha tanti elementi quanti sono i nodi del grafo, e $C[u]=C[v]⟺$ $u$ e $v$ sono nella stessa componente connessa.

Per l’esempio sopra, il vettore sarebbe:

$C=\begin{array}{ccccccccccccccccccc}1& 2& 1& 3& 4& 5& 1& 2& 2& 2& 1& 3& 5& 2& 5& 2& 1& 5& 3\end{array}$

algoritmo per il vettore delle componenti connesse:

def Componenti(x, G, C, c):
	C[x] = c
	for y in G[x]:
		if C[y] == 0:
			Componenti(y, G, C, c)
 
def main(G):
	C = [0]*len(G)
	c = 0
	for x in range(len(G)):
		if C[x] == 0:
			c+=1
			Componenti(x, G, C, c)
	return C

• questo algoritmo ha complessità $O(n+m)$

componente fortemente connessa

Una componente fortemente connessa di un grafo diretto è un sottografo composto da un insieme massimale di nodi connessi da cammini.

grafo fortemente connesso

Come per i grafi indiretti, un grafo diretto si dice fortemente connesso se ha una sola componente.

• un grafo fortemente connesso con più di un nodo è sempre ciclico

grafo fortemente connesso

• ogni nodo deve quindi essere raggiungibile da tutti gli altri nodi

esempio di grafo con 5 componenti:

$C=\begin{array}{cccccccccccc}1& 1& 2& 1& 1& 3& 1& 1& 4& 5& 4& 4\end{array}$

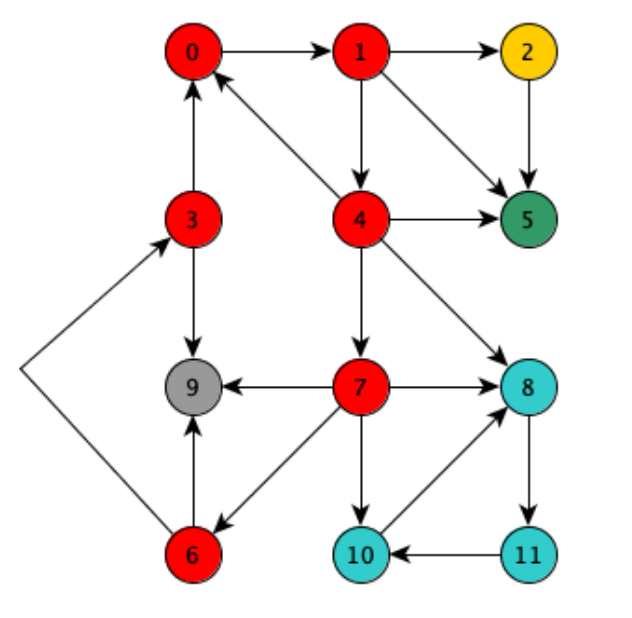
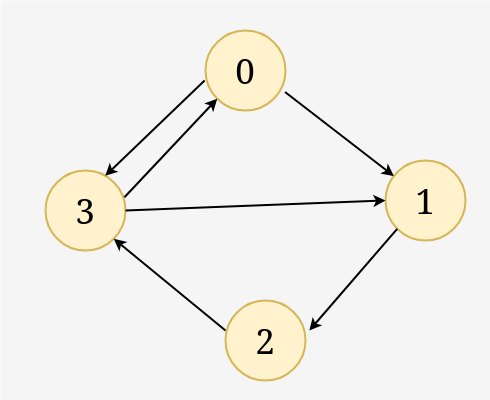
attenzione

l’algoritmo per le componenti connesse non funziona nel caso di componenti fortemente connesse: infatti, se c’è un cammino da $x$ a $y$, non è detto che ce ne sia anche uno da $y$ a $x$.

Per scrivere un algoritmo che, dato un grafo diretto $G$ ed un suo nodo $u$, calcola i nodi della componente fortemente connessa che contiene $u$, è utile creare il grafo trasposto $G^T$ di $G$.

grafo trasposto

Dato un grafo diretto $G$, il suo grafo trasposto $G^T$ ha gli stessi nodi di $G$, ma archi con direzione opposta.

(quindi, se facciamo una DFS a partire da un nodo $u$, otterremo tutti i nodi che, in $G$, portano a $u$)

algoritmo

Un possibile algoritmo per trovare il vettore delle componenti fortemente connesse funziona quindi così:

1. si calcola l’insieme $A$ dei nodi raggiungibili da $u$
   • semplice visita DFS
   • $O(n+m)$
2. si costruisce il grafo trasposto $G^T$
   • $O(n+m)$
3. si calcola l’insieme $B$ dei nodi che portano a $u$
   • visita DFS su $G^T$
   • $O(n+m)$
4. si restituisce l’intersezione dei due insiemi $A$ e $B$ - $\Theta (n)$
   • a questo punto si hanno due vettori dei visitati (con la stessa cardinalità) - si scorrono semplicemente gli indici e si controlla per quali nodi entrambi hanno valore $1$
   • $O(n)$

algoritmo per trovare la componente fortemente connessa di un nodo:

def ComponenteFC(x, G):
	visitati = DFS(x,G)
	GT = Trasposto(G)
	visitatiT = DFS(x, GT)
	
	componente = []
	for i in range(len(G)):
		if visitati[i] == visitatiT[i] == 1:
			componente.append(i)
	return componente

def Trasposto(G):
	GT = [ [] for _ in G]
	for i in range(len(G)):
		for v in G[i]:
			GT[v].append(i) 
# (metto il nodo sorgente nella lista di adiacenza del n. destinazione)
	return GT

questo algoritmo può essere usato come subroutine per trovare le componenti fortemente connesse di tutti i nodi:

algoritmo per trovare il vettore delle componenti FC:

def compFC(G):
	FC = [0]*len(G)
	c = 0
	for i in range(len(G)):
		if FC[i] == 0: 
			E = ComponenteFC(i, G) 
			# ^ ritorna un array con i numeri dei nodi nella comp.
			c+=1
			for x in E:
				FC[x] = c
	return FC

Al caso pessimo, la complessità sarà $O(n^3)$. Consideriamo il caso di un grafo diretto $G$ avente un arco $(u,v)$ per ogni $u\le v$.

• facciamo $n$ visite, di cui ognuna costa $O(n+m)$
• ma gli archi sono $\frac{n(n-1)}{2}=O(n^2)$, quindi:
• $O(n)\times O(n^2)=O(n^3)$

Esistono algoritmi che lavorano in tempo $O(n+m)$, come l’algoritmo di Tarjan e quello di Kosaraju (da aggiungere !! ma non in programma).